Prisma persegi

Kami menerangkan apa prisma kuadrangular, ciri -ciri, wajah, simpang, tepi, bagaimana mengira jumlah, contoh dan latihan yang diselesaikan

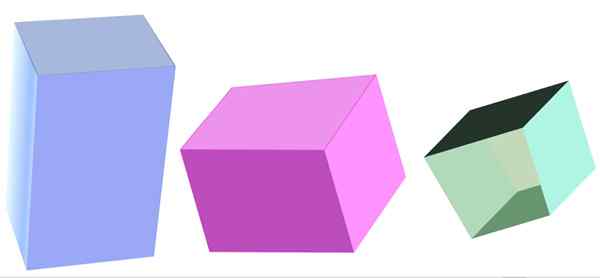
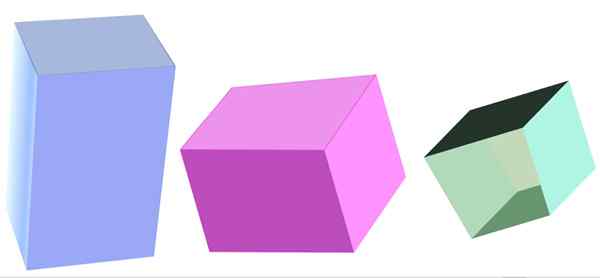Pelbagai jenis prisma kuadrangular. Sumber: f. Zapata

Apa itu prisma kuadrangular?

Dia Prisma persegi Ia adalah angka geometri tiga dimensi keluarga polyhedros. Ia terdiri daripada dua muka yang sama dan selari, dengan bentuk segi empat, sebagai pangkalan, dan empat paralelogram di sisi, untuk sejumlah enam muka.

Terdapat beberapa kriteria untuk mengklasifikasikannya, kerana terdapat banyak kemungkinan untuk bentuk wajah dan kecenderungan. Contohnya, ada Prisms Run Rumah Lurus dan juga prisma kuadrangular cenderung.

Dalam kes pertama, sisi berserenjang dengan pangkalan, dan kemudian mereka adalah segi empat tepat atau dataran. Dalam kes kedua, muka sebelah cenderung berkenaan dengan pangkalan, oleh itu, mereka tidak boleh menjadi segi empat tepat atau persegi.

Di samping itu, prisma kuadrangular boleh menjadi biasa atau tidak teratur, bergantung kepada asas adalah segi empat sama atau tidak teratur. Quadrilateral biasa adalah dataran, yang empat sisi dan empat sudutnya sama .

Contoh prisma rumah khas adalah parallelepiped, yang asasnya adalah selari. Bentuk kotak dan batu bata diilhamkan oleh prisma kuadrangular, contoh yang baik tentang cara menggunakan angka geometri ini dalam aplikasi praktikal adalah.

Ciri -ciri prisma kuadrangular

Antara ciri -ciri yang paling penting dalam prisma kuadrangular adalah seperti berikut:

• Wajah mereka mempunyai bentuk poligon.
• Ia mempunyai sejumlah 6 muka (2 pangkalan dan 4 sisi), 12 tepi atau tepi dan 8 simpang (sudut).
• Wajah sisi boleh dibentuk seperti: persegi, segi empat tepat, parallelogram, rhombus atau rhomboid.
• Sisinya boleh lurus (sudut 90º dengan pangkalan) atau cenderung (terdapat sudut kurang daripada 90º di bahagian dalaman).
• Wajah lateral prisma lurus hanya boleh menjadi persegi atau segi empat tepat.
• Pangkalan prisma juga menerima nama garis panduan.
• Sekiranya pangkalannya adalah segi empat segi biasa, prisma kuadrangular juga biasa. Sebagai angka rata adalah biasa jika semua sisinya mempunyai ukuran yang sama, satu -satunya kemungkinan adalah bahawa pangkalannya adalah persegi.
• Apabila pangkal prisma adalah segi empat sama lain yang berbeza dari dataran, maka prisma dianggap tidak teratur.
• Prisma Quadrangular biasa boleh didaftarkan dalam silinder.

Boleh melayani anda: Statistik inferens: sejarah, ciri, apa itu, contohnya

Unsur Prisma Quadrangular

Lima elemen prisma kuadrangular adalah perkara biasa bagi semua prisma:

• Pangkalan, dibentuk oleh dua kuadrilaterals yang sama dan selari.
• Muka sisi, adalah empat paralelogram yang sempadan angka itu.
• Simpang atau sudut, titik umum yang mempunyai tiga sisi bersebelahan prisma.
• Tepi atau tepi, segmen biasa yang mempunyai dua wajah bersebelahan.
• Ketinggian: Ia adalah panjang segmen tegak lurus dengan hujung di pangkalan. Apabila prisma lurus, ketinggian bertepatan dengan ukuran tepi sisi.
• Seksyen lurus, kawasan persimpangan antara prisma dan satah yang membentuk 90º dengan tepi sampingan.

Imej berikut menunjukkan setiap elemen ini untuk prisma kuadrat lurus:

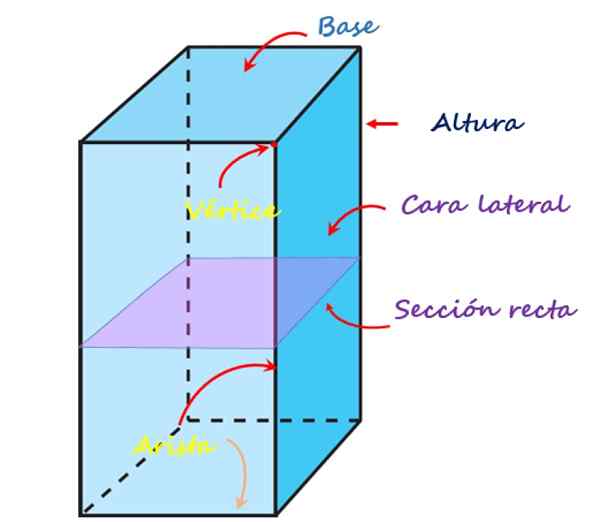Unsur -unsur prisma kuadrangular. Sumber: f. Zapata

Wajah, simpang dan tepi

Yang sangat penting untuk mengkaji prisma kuadrangular adalah wajah, simpang dan tepi:

Muka

Wajah prisma membuat jumlah 6: 2 pangkalan yang sama dalam bentuk segi empat dan sisi 4 sisi atau wajah dalam bentuk parallelogram.

Simpang

Mereka adalah sudut angka, titik di mana tiga wajah bersebelahan datang.

Tepi

Mereka adalah segmen persimpangan antara wajah prisma. Tepi diklasifikasikan sebagai:

• Tepi asas, Segmen biasa antara pangkalan dan muka sisi.
• Tepi sisi, Seperti namanya, mereka adalah segmen biasa di antara muka sebelah.

Angka teratas menunjukkan dua jenis tepi, yang ditetapkan dengan anak panah warna yang berbeza. Bilangan tepi n_Ke boleh ditentukan dengan Teorem Euler daripada polyhedros, yang mengaitkan bilangan tepi dengan wajah n_C dan simpang n_V:

Boleh melayani anda: fungsi matematik

N_Ke = N_C + N_V -2

Untuk prisma kuadrangular n_C = 6 dan n_V = 8, oleh itu:

N_Ke = 6 + 8 -2 = 12

Oleh itu, bilangan tepi atau tepi prisma kuadrangular ialah 12.

Cara mengira jumlah prisma kuadrangular?

Jumlah prisma difahami sebagai sebahagian daripada ruang yang dikunci olehnya, dan diukur dalam unit padu, yang boleh menjadi meter padu, sentimeter padu, kaki padu atau lain -lain yang sesuai, dengan syarat mereka panjang ke kubus.

Volum V adalah jumlah yang positif, dan dalam hal mana -mana prisma kuadrangular, ia diberikan oleh produk antara pangkal pangkalan ke_b dan ketinggian h:

V = a_b × h

Yo) Jumlah prisma kuadrangular biasa

Oleh kerana pangkalannya adalah persegi, dan persegi dataran adalah ℓ persegi:

Ke_b = ℓ²

Kemudian, jumlah prisma yang ketinggiannya adalah "H" adalah:

V = ℓ² × h

Ii) Jumlah prisma kuadrangular yang tidak teratur

Ia bergantung kepada bentuk asas dan ketinggian "H" prisma:

1.- Prisma asas segi empat tepat

Kawasan segi empat tepat "A" dan "B" adalah:

Ke_b = A × b

Jadi kelantangannya ialah:

V = a × b × h

2.- Prisma asas romboidal

Kawasan Rhombus adalah produk separuh daripada pepenjuru "d" dan "d":

Dan jumlahnya ialah:

3.- Romboid -Prisma Pangkalan Berbaring

Kawasan asas berbentuk rhomboid adalah produk asasnya "b" dan ketinggian relatifnya "h_r"Ke pangkalan ini, yang merupakan segmen tegak lurus yang pergi dari pangkalan ini ke sisi selari dengannya.

Ke_b = B × h_r

Oleh itu, jumlah prisma dengan pangkalan ini adalah:

Boleh melayani anda: berapakah julat statistik? (Dengan contoh)

V = b × h_r × h

4.- Prisma asas trapezoid

Oleh kerana kawasan trapezoid adalah separuh tapak selari "A" dan "B", didarabkan dengan ketinggiannya "C":

Jumlah prisma trapezoid adalah:

5.- Prisma asas berbentuk trapezoid

Kawasan trapezoid simetri adalah separuh produk pepenjuru d dan d, oleh itu:

Dalam kes ini, jumlah prisma adalah:

Latihan diselesaikan

Prisma Quadrangular asas trapezoid mempunyai jumlah 648 cm³. Sisi selari ukuran trapezoid a = 10 cm dan b = 5 cm, manakala ketinggian trapeze ialah c = 6 cm. Dengan data ini dapatkan ketinggian prisma.

Penyelesaian

Oleh kerana dimensi asasnya, kawasan anda dapat dikira dengan mudah:

Dan formula:

V = a_b × h

"H" dibersihkan, ketinggian prisma, kerana jumlahnya diketahui:

H = v/ a_b = 648 cm³ / 45 cm² = 14.4 cm

Contoh

Prisma atau kiub segi empat tepat

Enam muka prisma lurus ini adalah persegi atau segi empat tepat. Kotak adalah contoh prisma segi empat tepat, bentuk yang juga digunakan dalam pelbagai objek dan pembinaan seperti bangunan.

Kiub

A Cube adalah prisma kuadrangular biasa, yang enam sisinya dibentuk seperti persegi, contohnya, dadu atau permainan kiub Rubik yang terkenal.

Kubus adalah sebahagian daripada kumpulan pepejal platonik, angka geometri yang memenuhi dua syarat. Yang pertama adalah bahawa setiap muka adalah poligon biasa dan yang kedua adalah bahawa setiap puncak mempunyai persamaan bilangan wajah yang sama.

Kubus memenuhi kedua -dua keadaan, kerana wajah mereka mempunyai bentuk persegi, yang merupakan poligon biasa. Dan di setiap lapan simpang kiub tiga muka yang sama berkumpul.

Pepejal platonik yang tersisa adalah tetrahedron, octahedron, dodecahedro dan icosaedro.