Apakah percubaan deterministik?

Dia Eksperimen deterministik, Dalam statistik, ia adalah satu yang mempunyai hasil yang boleh diramalkan dan boleh dihasilkan selagi keadaan awal dan parameter yang sama dikekalkan. Iaitu, hubungan sebab-akibatnya diketahui secara keseluruhan.

Contohnya, masa yang mengambil pasir dari satu jam untuk bergerak dari satu petak ke yang lain adalah percubaan deterministik, kerana hasilnya dapat diramalkan dan boleh dihasilkan. Selagi keadaannya sama, ia akan mengambil masa yang sama untuk bergerak dari kapsul ke kapsul.

Rajah 1. Masa yang mengambil pasir dari satu petak ke yang lain adalah percubaan deterministik. Sumber: Pixabay

Banyak fenomena fizikal adalah deterministik, beberapa contoh yang berikut:

- Objek paling padat daripada air, seperti batu, akan selalu tenggelam.

- Float, yang kurang padat daripada air, akan sentiasa bertahan (kecuali jika daya yang membuatnya tenggelam) dilaksanakan).

- Suhu mendidih air di paras laut selalu 100 ºC.

- Masa yang diperlukan untuk jatuh yang diberikan yang jatuh dari rehat, kerana ia ditentukan oleh ketinggian dari mana ia jatuh dan kali ini selalu sama (apabila ia dibebaskan dari ketinggian yang sama).

Mengambil kesempatan daripada contoh dadu. Sekiranya ini dijatuhkan, walaupun anda berhati -hati untuk memberikan orientasi yang sama dan selalu pada ketinggian yang sama, sukar untuk meramalkan wajah yang akan muncul setelah ia berhenti di tanah. Ini akan menjadi percubaan rawak.

Secara teorinya, jika mereka dikenali dengan data ketepatan tak terhingga seperti: kedudukan; orientasi kelajuan dan dadu awal; bentuk (tepi bulat atau sudut); dan pekali pemulihan permukaan di mana ia jatuh, mungkin mungkin untuk meramalkan, melalui pengiraan yang kompleks, apa yang dihadapi dadu akan ditunjukkan apabila ia berhenti. Tetapi apa -apa variasi kecil dalam keadaan permulaan akan memberikan hasil yang berbeza. 

Sistem sedemikian adalah deterministik dan pada masa yang sama huru -hara, kerana perubahan kecil keadaan awal mengubah hasil akhir dengan cara rawak.

Boleh melayani anda: Sistem Persamaan: Kaedah Penyelesaian, Contoh, Latihan

[TOC]

Pengukuran

Eksperimen deterministik dapat diukur sepenuhnya, tetapi masih pengukuran hasilnya tidak tepat dan mempunyai margin tertentu ketidakpastian.

Mari kita letakkan sebagai contoh percubaan berikut, benar -benar deterministik: Lepaskan kereta mainan di lereng lurus.

Rajah 2. Sebuah kereta turun melalui cerun rectilinear dalam eksperimen deterministik. Sumber: Pixabay.

Selalu dibebaskan dari titik permulaan yang sama, berhati -hati untuk tidak memberi impuls. Dalam kes ini, masa yang mengambil kereta untuk mengembara trek mestilah sama.

Sekarang seorang kanak -kanak berhasrat untuk mengukur masa yang dia ambil ke kereta trek trek. Untuk ini anda akan menggunakan jam randik yang dimasukkan ke dalam telefon bimbit anda.

Menjadi budak pemerhati, perkara pertama yang anda perhatikan ialah instrumen pengukuran anda mempunyai ketepatan terhingga, kerana perbezaan masa yang sedikit yang dapat mengukur jam randik adalah 1 ratus saat.

Kemudian kanak -kanak itu meneruskan eksperimen dan dengan langkah -langkah jam randik mudah alih 11 kali - katakanlah bahawa untuk memastikan - masa yang dia ambil ke kereta dorong untuk mengembara pesawat cenderung, mendapatkan hasil berikut:

3,12S 3.09S 3.04S 3.04S 3.10S 3.08S 3.05S 3.10s 3.11s 3.06s dan 3.03s.

Kanak -kanak itu terkejut, kerana di sekolah mereka telah memberitahunya bahawa ini adalah percubaan deterministik, tetapi pada setiap tahap dia memperoleh hasil yang sedikit berbeza.

Variasi sejauh mana

Apa yang boleh menjadi punca yang dalam setiap pengukuran mempunyai hasil yang berbeza? 

Sebab boleh menjadi ketepatan instrumen, yang telah dikatakan adalah 0.01s. Tetapi perhatikan bahawa perbezaan dalam pengukuran adalah di atas nilai itu, jadi ia harus dianggap sebagai sebab -sebab lain, seperti:

- Variasi kecil titik permulaan.

- Perbezaan pada awal dan berhenti jam randik, kerana masa reaksi kanak -kanak.

Mengenai masa tindak balas, kelewatan pasti berlaku kerana kanak -kanak melihat bahawa kereta itu mula bergerak, sehingga jam randik menekan. 

Boleh melayani anda: tepi kubus

Begitu juga, pada ketibaan terdapat kelewatan kerana masa untuk reaksi. Tetapi kelewatan permulaan dan ketibaan dikompensasi, sehingga masa yang diperoleh mestilah sangat dekat dengan yang nyata. 

Walau apa pun, pampasan untuk kelewatan tindak balas tidak tepat, kerana masa tindak balas boleh mempunyai variasi kecil dalam setiap percubaan, yang menjelaskan perbezaan hasilnya.

Apa yang sebenarnya hasil eksperimen sebenar?

Keputusan pengukuran dan kesilapan

Untuk melaporkan hasil akhir kita mesti menggunakan statistik. Pertama mari kita lihat seberapa kerap hasilnya diulang:

- 3.03s (1 kali)

- 3.04s (2 kali)

- 3.05s (1 kali)

- 3.06s (1 kali)

- 3.08s (1 kali)

- 3.09s 1 kali

- 3.10s (2 kali)

- 3.11s (1 kali)

- 3.12s (1 kali)

Semasa memesan data, kami menyedari bahawa a fesyen atau lebih banyak hasil berulang. Kemudian hasilnya melaporkan adalah aritmetik, yang boleh dikira seperti berikut:

(1 × 3.03 + 2 × 3.04 + 1 × 3.05 + 1x 3.06 + 1 × 3.08 + 1 × 3.09 + 2 × 3.10 + 1 × 3.11 + 1 × 3,12) / (1 + 2 + 1 + 1 + 1 + 1 + 2 + 1 + 1).

Hasil pengiraan sebelumnya ialah 3.074545455. Secara logiknya, tidak masuk akal untuk melaporkan semua perpuluhan ini, kerana setiap pengukuran tidak mempunyai 2 perpuluhan ketepatan. 

Memohon peraturan pembulatan, boleh dikatakan bahawa masa yang diperlukan untuk lawatan kereta trek adalah aritmetik bulat untuk dua angka perpuluhan.

Hasilnya yang boleh kita laporkan untuk eksperimen kami ialah:

3.08 saat adalah masa yang anda bawa ke kereta mainan perjalanan trek yang cerah.

- Ralat pengukuran

Seperti yang dilihat dalam contoh eksperimen deterministik kami, setiap pengukuran mempunyai ralat, kerana ia tidak dapat diukur dengan ketepatan tak terhingga.

Walau apa pun, satu -satunya perkara yang boleh dilakukan adalah untuk meningkatkan kaedah instrumen dan pengukuran, untuk mendapatkan hasil yang lebih tepat.

Di bahagian sebelumnya, kami memberikan hasil untuk eksperimen deterministik kami pada masa yang diperlukan untuk kereta mainan untuk mengembara trek cenderung. Tetapi hasil ini membayangkan kesilapan. Sekarang kita akan menerangkan cara mengira ralat itu.

Ia dapat melayani anda: koordinat segi empat tepat: contoh dan latihan diselesaikan

- Pengiraan ralat pengukuran

Dalam pengukuran untuk masa terdapat penyebaran dalam langkah -langkah yang dibuat. The sisihan piawai Ini adalah borang statistik yang sering digunakan untuk melaporkan penyebaran data. 

Varians dan sisihan piawai

Cara untuk mengira sisihan piawai adalah seperti ini: pertama adalah varians data, yang ditakrifkan dengan cara ini:

Jumlah perbezaan setiap hasil dengan purata aritmetik, kuadrat dan dibahagikan dengan jumlah data

Sekiranya akar kuadrat diambil ke varians, sisihan piawai kemudian diperolehi.

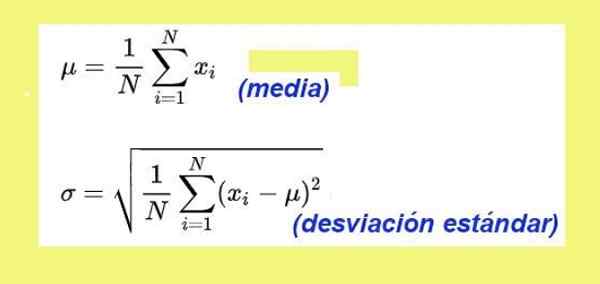Rajah 3. Formula purata dan sisihan piawai. Sumber: Wikimedia Commons.

Penyimpangan piawai untuk data masa keturunan mainan auton adalah:

σ = 0.03

Hasilnya dibulatkan kepada 2 perpuluhan, kerana ketepatan setiap data adalah 2 perpuluhan. Dalam kes ini 0.03s mewakili ralat statistik setiap data.

Walau bagaimanapun, purata aritmetik purata masa yang diperolehi mempunyai ralat yang lebih rendah. Ralat purata dikira dengan membahagikan sisihan piawai antara akar kuadrat jumlah nombor data.

Ralat purata = σ / √n = 0.03 / √11 = 0.01

Ia.

Sebagai hasil akhir dari langkah itu, dilaporkan kemudian:

 T = 3.08s ± 0.01s adalah masa yang diperlukan untuk kereta mainan untuk mengembara trek cenderung.

Disimpulkan bahawa walaupun ia datang kepada percubaan deterministik, hasil pengukurannya tidak mempunyai ketepatan tak terhingga dan selalu mempunyai margin kesilapan. 

Dan di samping itu, untuk melaporkan hasil akhir, ia perlu, walaupun ia berkaitan dengan percubaan deterministik, gunakan kaedah statistik.

Rujukan

1. Canalphi. Eksperimen deterministik. Pulih dari: youtube.com
2. Mathemovil. Eksperimen deterministik. Pulih dari: youtube.com
3. Pishro Nick h . Pengenalan kepada kebarangkalian. Diperolehi daripada: ProbabilityCourse.com
4. Ross. Kebarangkalian dan statistik untuk jurutera. Mc-Graw Hill.
5. Statistik bagaimana. Deterministik: Definisi dan peperiksaan. Pulih dari: statistikshowto.DatascienceCeral.com
6. Wikipedia. Penyimpangan biasa. Pulih dari: Adakah.Wikipedia.com
7. Wikipedia. Eksperimen (teori kebarangkalian). Diperoleh dari: dalam.Wikipedia.com