Peraturan tangan kanan

Rajah 1. Peraturan tangan kanan. Sumber: Wikimedia Commons. ACDX [cc by-s (http: // creativeCommons.Org/lesen/by-sa/3.0/]].

Apakah peraturan tangan kanan?

The peraturan tangan kanan Ia adalah sumber mnemonik untuk menubuhkan arah dan arah vektor yang dihasilkan dari produk vektor atau produk silang. Ia digunakan secara meluas dalam fizik, kerana terdapat magnitud vektor penting yang merupakan hasil dari produk vektor. Begitu juga dengan tork, daya magnet, momentum sudut dan momen magnet, sebagai contoh.

Menjadi dua vektor generik ke dan b produk salib yang ke x b. Modul vektor sedemikian adalah:

ke x b = ke.b.dosa α

Di mana α adalah sudut minimum antara ke dan b, Sementara A dan B mewakili modul mereka. Untuk membezakan vektor dari modul mereka, huruf berani digunakan.

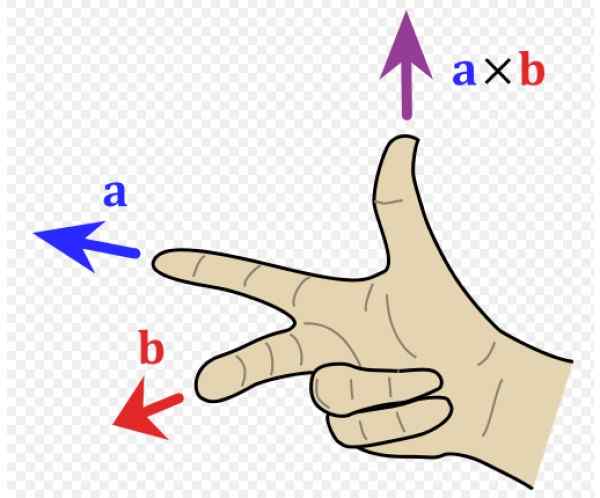
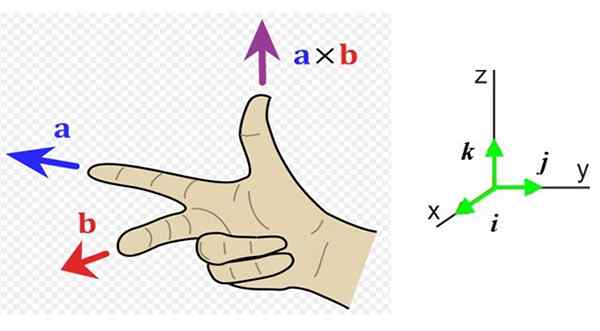
Sekarang kita perlu mengetahui arah dan makna vektor ini, jadi mudah untuk mempunyai sistem rujukan dengan tiga arah ruang (Rajah 1 kanan). Vektor unit Yo, J dan k Masing -masing menunjuk kepada pembaca (keluar dari halaman), ke kanan dan ke atas.

Dalam contoh Rajah 1 kiri, vektor ke menuju ke kiri (alamat dan jari negatif dan indeks tangan kanan) dan vektor b pergi ke pembaca (alamat x positif, jari tengah tangan kanan).

Vektor yang dihasilkan ke x b mempunyai arah ibu jari, ke arah z positif.

Peraturan kedua tangan kanan

Peraturan ini banyak digunakan apabila terdapat magnitud yang arah dan makna berputar, seperti medan magnet B dihasilkan oleh dawai nipis dan rectilinear yang mengangkut arus.

Dalam kes ini, garis medan magnet adalah lilitan sepusat dengan dawai, dan arah gilirannya diperoleh dengan peraturan ini seperti berikut: ibu jari kanan menunjukkan arah arus dan empat jari yang tersisa adalah melengkung ke arah arah arah bidang. Kami menggambarkan konsep dalam Rajah 2.

Boleh melayani anda: kejutan elastik: dalam dimensi, kes khas, latihan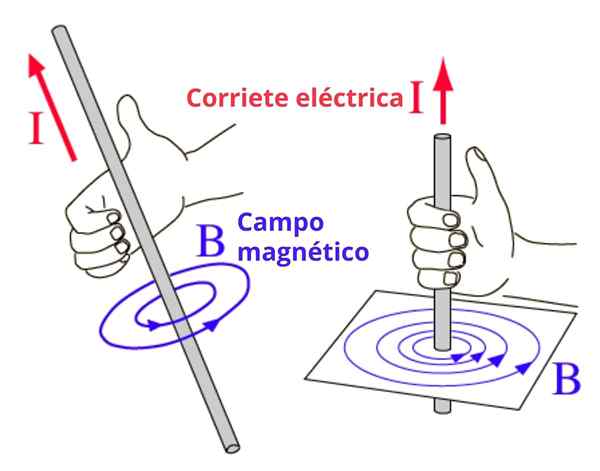Rajah 2. Peraturan tangan kanan untuk menentukan makna peredaran medan magnet

Peraturan alternatif tangan kanan

Angka berikut menunjukkan bentuk alternatif peraturan tangan kanan. Vektor yang muncul dalam pencerahan adalah:

• Kelajuan v beban tepat waktu itu.
• Medan magnet B di mana beban bergerak.
• F_B Daya yang dimaklumkan oleh medan magnet pada beban.

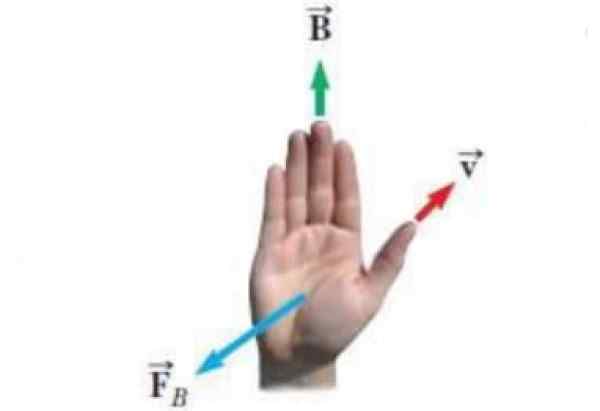Rajah 3. Peraturan alternatif tangan kanan. Sumber: Wikimedia Commons. EXPERICUIS [CC BY-SA (https: // creativeCommons.Org/lesen/by-sa/4.0)]

Persamaan untuk daya magnet adalah F_B = Qv x B dan peraturan tangan kanan untuk mengetahui arah dan rasa F_B Ia terpakai seperti ini: Titik ibu jari mengikut V, baki empat jari diletakkan mengikut bidang b. Jadi F_B Ia adalah vektor yang keluar dari telapak tangan, tegak lurus, seolah -olah ia menolak beban.

Perhatikan bahawa F_B akan menunjuk ke arah yang bertentangan jika beban yang negatif, kerana produk vektor tidak komutatif. Sebenarnya:

ke x B = - b x ke

Aplikasi

Peraturan tangan kanan boleh digunakan untuk pelbagai magnitud fizikal, mari kita tahu beberapa dari mereka:

Kelajuan dan percepatan sudut

Kedua -dua halaju sudut Ω Seperti pecutan sudut α Mereka adalah vektor. Sekiranya objek berputar di sekitar paksi tetap, kemungkinan halaju sudut Ω.

Bagi bahagiannya pecutan sudut α akan mempunyai alamat yang sama seperti Ω, Tetapi maknanya bergantung pada jika Ω meningkatkan atau mengurangkan magnitudnya dari masa ke masa. Dalam kes pertama, kedua -duanya mempunyai arah dan makna yang sama, tetapi pada kedua mereka akan mempunyai deria bertentangan.

Boleh melayani anda: Undang -undang Watt: Apa, Contoh, Aplikasi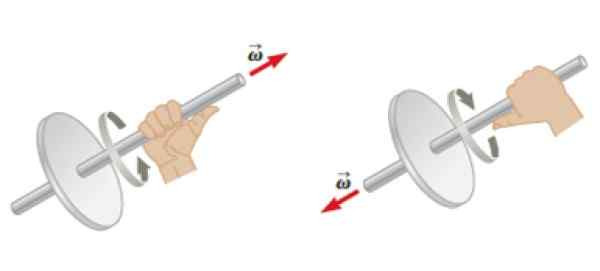Rajah 4. Peraturan tangan kanan digunakan pada objek dalam putaran untuk menentukan arah dan arah halaju sudut. Sumber: Serway, r. Fizikal.

Momentum sudut

Vektor sudut L_{Sama ada} zarah yang berputar di sekitar paksi tertentu atau ditakrifkan sebagai produk vektor vektor kedudukan segera r  dan jumlah pergerakan linear p:

L = r x p

Peraturan kanan diterapkan dengan cara ini: jari telunjuk diletakkan ke arah dan arah yang sama r, Jari tengah di p, kedua -duanya di atas kapal terbang mendatar, seperti dalam angka. Secara automatik, ibu jari meluaskan secara menegak ke atas menunjuk arah dan arah momentum sudut L_{Sama ada.}

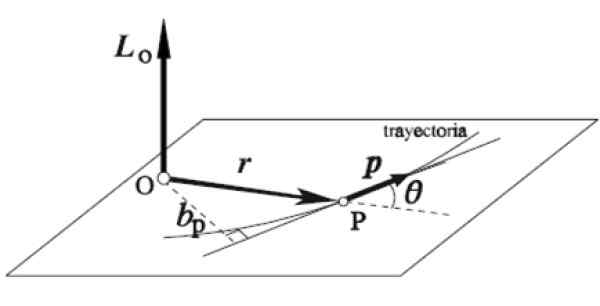Rajah 5. Vektor sudut. Sumber: Wikimedia Commons.

Latihan

Latihan 1

Putaran Rajah 6 akan cepat dengan halaju sudut Ω dan paksi simetrinya pecah lebih perlahan di sekitar paksi menegak z. Pergerakan ini dipanggil Precession. Terangkan kekuatan yang bertindak pada putaran dan kesannya menghasilkan.

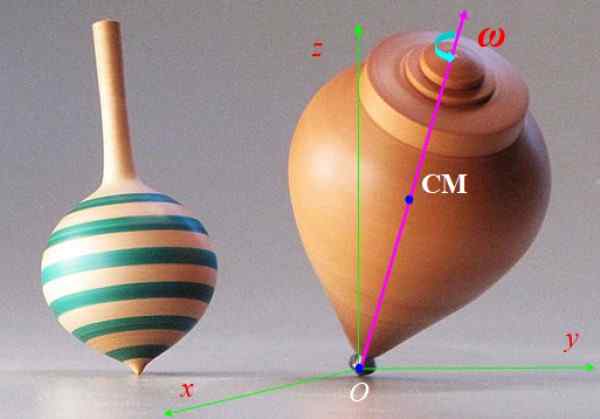Rajah 6. Berputar berputar. Sumber: Wikimedia Commons.

Penyelesaian

Daya yang bertindak pada putaran adalah normal N, digunakan pada titik sokongan dengan tanah atau lebih berat mg, digunakan di tengah -tengah massa cm, dengan g Vektor pecutan keparahan, diarahkan secara menegak (lihat Rajah 7).

Kedua -dua kuasa itu seimbang, oleh itu putaran tidak bergerak. Namun beratnya menghasilkan tork atau tork τ Bersih mengenai titik atau, diberikan oleh:

τ_{Sama ada} = r_{Sama ada} x F, dengan F = Mg.

Sebagai r dan mg Mereka sentiasa berada di dalam kapal terbang ketika putaran berputar, menurut pemerintahan tangan kanan tork τ_{Sama ada} Ia selalu terletak di dalam kapal terbang Xy, tegak lurus kedua -dua a r sebagai g.

Perhatikan bahawa N tidak menghasilkan tork berkenaan dengan O, kerana vektornya r Mengenai atau batal. Tork itu menghasilkan perubahan dalam momentum sudut yang menyebabkan precession putaran di sekitar paksi z.

Boleh melayani anda: Baki termodinamik: Kelas dan aplikasi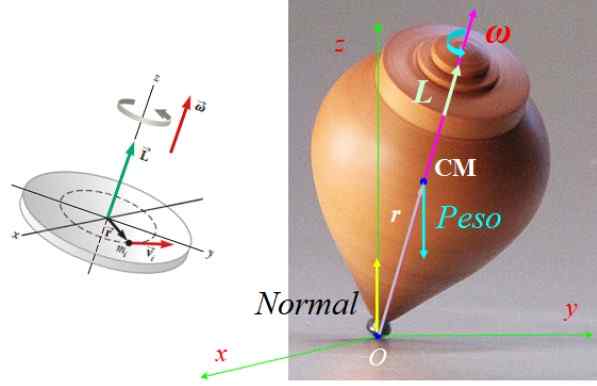Rajah 7. Kekuatan yang bertindak pada putaran dan vektor momentum sudutnya. Sumber Rajah Kiri: Serway, r. Fizik untuk Sains dan Kejuruteraan.

Latihan 2

Tunjukkan arah dan arah vektor momentum sudut L dari Trumpe Rajah 6.

Penyelesaian

Mana -mana titik putaran mempunyai massa m_Yo, kelajuan v_Yo dan kedudukan vektor r_Yo, Apabila ia berkisar di sekitar paksi z. Momentum sudut L_Yo zarah tersebut adalah:

L_Yo = r_Yo x p_Yo = r_Yo x m_Yov_Yo

Diberi r_Yo dan v_Yo Mereka berserenjang, magnitud L adalah:

L_Yo = m_Yor_Yov_Yo

Kelajuan linear v berkaitan dengan halaju sudut Ω melalui:

v_Yo = r_YoΩ

Oleh itu:

L_Yo = m_Yor_Yo (r_YoΩ) = m_Yor_Yo²Ω

Jumlah momentum sudut trompo L adalah jumlah momentum sudut setiap zarah:

L = (Σm_Yor_Yo² ) Ω

Σ m_Yor_Yo²  Ia adalah momen inersia i dari putaran, maka:

L= IΩ

Oleh itu L dan Ω Mereka mempunyai arah dan makna yang sama, seperti yang ditunjukkan dalam Rajah 7.