Teorem Asas Demonstrasi Aritmetik, Aplikasi, Latihan

Dia Teorem asas aritmetik Dia menyatakan bahawa mana -mana bilangan semula jadi lebih besar daripada 1 dapat dipecahkan sebagai produk nombor perdana - memegang beberapa - dan borang ini unik untuk nombor itu, walaupun urutan faktor dapat berbeza.

Ingat bahawa nombor utama p Ia adalah yang hanya mengakui sebagai pembahagi positif itu sendiri dan 1. Nombor berikut adalah sepupu: 2, 3, 5, 7, 11, 13 dan sebagainya, kerana terdapat tak terhingga. Nombor 1 tidak dianggap sepupu, kerana mempunyai pembahagi tunggal.

Rajah 1. Euclides (kiri) menunjukkan teorem asas aritmetik dalam elemen bukunya (350 a.C.), Dan demonstrasi lengkap pertama adalah disebabkan oleh Carl f. Gauss (1777-1855) (betul). Sumber: Wikimedia Commons.

Bagi mereka, nombor yang tidak memenuhi perkara di atas dipanggil nombor terdiri, Sebagai 4, 6, 8, 9, 10, 12, 14 ... Mari ambil nombor 10 sebagai contoh dan segera kita melihat bahawa ia boleh dipecahkan sebagai produk 2 dan 5:

10 = 2 × 5

Kedua -dua 2 dan 5 memang, nombor utama. Teorem menyatakan bahawa ini mungkin untuk nombor n:

Di mana p₁, p₂, p₃... p_r Mereka nombor utama dan k₁, k₂, k₃,... k_r Mereka adalah nombor semula jadi. Jadi nombor perdana bertindak seperti batu bata dari mana, dengan pendaraban, bilangan semula jadi dibina.

[TOC]

Demonstrasi teorem asas aritmetik

Ia mula menunjukkan bahawa setiap nombor dapat terurai dalam faktor utama. Jadilah nombor semula jadi n> 1, sepupu atau kompaun.

Contohnya jika n = 2, ia boleh dinyatakan sebagai: 2 = 1 × 2, iaitu sepupu. Dengan cara yang sama kita meneruskan dengan nombor berikut:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Kami terus seperti ini, menguraikan semua nombor semula jadi sehingga kami mencapai nombor n -1. Mari kita lihat sama ada kita boleh melakukannya dengan nombor yang berikut: n.

Jika n adalah sepupu, kita boleh menguraikannya sebagai n = 1 × n, tetapi anggap bahawa n disusun dan mempunyai pembahagi d, secara logiknya kurang daripada n:

Boleh melayani anda: Statistik deskriptif: sejarah, ciri, contoh, konsep

1< d < n.

Ya n/d = p₁, dengan p₁ Nombor Perdana, maka N ditulis sebagai:

n = p₁.d

Sekiranya D adalah sepupu tidak ada yang perlu dilakukan, tetapi jika tidak, ada nombor n₂ yang merupakan pembahagi d dan kurang daripada ini: n₂ < d, por lo que d podrá escribirse como el producto de n₂ Untuk nombor sepupu lain p₂:

d = p₂ n₂

Bahawa dengan menggantikan nombor asal N akan memberi:

n = p₁ .p₂ .n₂

Sekarang anggap n₂ Juga tidak ada nombor perdana dan kami menulisnya sebagai produk nombor utama p₃, untuk pembahagi beliau₃, seperti n₃ < n₂ < n₁ < n:

n₂ = p₃.n₃ → n = p₁ p₂ p₃.n₃

 Kami mengulangi prosedur ini beberapa kali sehingga anda mendapat:

n = p₁.p₂.p₃ ... p_r

Ini bermakna bahawa adalah mungkin untuk menguraikan semua nombor keseluruhan dari 2 hingga nombor n, sebagai produk nombor perdana.

Keunikan penguraian dalam faktor utama

Mari kita sahkan sekarang bahawa kecuali perintah faktor, penguraian ini unik. Katakan anda boleh menulis dalam dua cara:

n = p₁.p₂.p₃ ... p_r = Q_1.q₂.q₃... q_s  (dengan r ≤ s)

Sudah tentu q₁, q₂, q₃... mereka juga nombor utama. Sebagai p₁ membahagikan kepada (q_1.q₂.q₃... q_s) Kemudian p₁ Ia sama dengan mana -mana "q", tidak kira Yang, jadi kita boleh mengatakan bahawa p₁ = Q₁. Kita membahagikan n antara p₁ Dan kita dapat:

p₂.p₃ ... p_r =_.q₂.q₃... q_s

Kami mengulangi prosedur untuk membahagikan segala -galanya antara p_r, Kemudian kita dapat:

1 = Q_R+1... q_s

Tetapi tidak mungkin untuk sampai ke Q_R+1... q_s = 1 Apabila r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Aplikasi

Seperti yang telah kami katakan sebelum ini, nombor utama mewakili jika anda mahu, atom -atom nombor, komponen asas mereka. Jadi teorem asas aritmetik mempunyai banyak aplikasi, yang paling jelas: kita boleh bekerja lebih mudah dengan bilangan besar jika kita menyatakannya sebagai hasil dari nombor yang lebih kecil.

Boleh melayani anda: keseluruhan nombor

Dengan cara yang sama, kita dapat mencari pelbagai maksimum (m.c.m.) dan pembahagi biasa maksimum (m.C.D.), Prosedur yang membantu kita membuat jumlah pecahan lebih mudah, mencari akar bilangan besar, atau beroperasi dengan radikal, merasionalisasi dan menyelesaikan masalah penggunaan sifat yang sangat pelbagai.

Di samping itu, nombor perdana sangat enigmatic. Corak belum diiktiraf di dalamnya dan tidak mungkin mengetahui apa yang akan berlaku. Yang terbesar sehingga masa ditemui oleh komputer dan mempunyai 24.862.048 Digit, Walaupun nombor perdana baru kelihatan kurang kerap setiap kali.

Nombor Primo dalam Alam

Cicadas, Cycaked atau Chicharras yang tinggal di timur laut Amerika Syarikat muncul dalam kitaran 13 atau 17 tahun. Kedua -duanya adalah nombor utama.

Dengan cara ini, Chicharras mengelakkan bertepatan dengan pemangsa atau pesaing yang mempunyai tempoh kelahiran yang lain, ataupun pelbagai jenis Chicharra bersaing antara satu sama lain, kerana mereka tidak bertepatan pada tahun yang sama.

Rajah 2. Cicada del Este dari Amerika Syarikat muncul setiap 13 atau 17 tahun. Sumber: Pxfuel.

Nombor primo dan pembelian dalam talian

Nombor primo digunakan dalam kriptografi untuk memastikan butiran kad kredit apabila anda membeli pembelian dalam talian. Dengan cara ini, data yang pembeli tiba tepat ke kedai tanpa tersesat atau jatuh ke dalam orang yang tidak bertanggungjawab.

Sebagai? Data kad dikodkan dalam nombor n yang boleh dinyatakan sebagai produk nombor perdana. Nombor Perdana ini adalah kunci yang mendedahkan data, tetapi mereka tidak diketahui oleh orang ramai, mereka hanya boleh dikodkan di web yang diarahkan.

Mengurangkan nombor ke dalam faktor adalah tugas yang mudah jika angka -angka kecil (melihat latihan diselesaikan), tetapi dalam hal ini ia digunakan sebagai bilangan utama utama 100 digit, yang dengan mendarabkan mereka memberikan angka yang lebih besar, yang penguraian terperinci menyiratkan a kerja besar.

Boleh melayani anda: anggaran tepat waktu

Latihan yang diselesaikan

- Latihan 1

Terurai 1029 menjadi faktor utama.

Penyelesaian

1029 boleh dibahagikan dengan 3. Dikenali kerana dengan menambahkan digit anda jumlahnya adalah berganda 3: 1+0+2+9 = 12. Oleh kerana urutan faktor tidak mengubah produk, kita boleh memulakannya:

1029 3

343

1029 = 3 × 343

Sebaliknya 343 = 7³, Jadi:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

Dan kerana kedua -dua 3 dan 7 adalah nombor utama, ini adalah penguraian 1029.

- Latihan 2

Faktor trinomial x² + 42x + 432.

Penyelesaian

Trinomial ditulis semula dalam bentuk (x+a). (x+b) dan kita perlu mencari nilai a dan b, supaya:

A+B = 42; ke.B = 432

Nombor 432 terurai menjadi faktor utama dan dari sana ia dipilih, oleh Tanteo, kombinasi yang sesuai untuk fakta yang ditambah kepada 42.

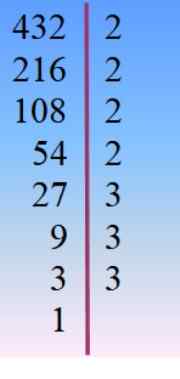
432 = 2⁴ × 3³ = 23³× 2³ = 2⁴× 3² × 3 = ..

Dari sini terdapat beberapa kemungkinan untuk menulis 432:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72 .. .

Dan semua boleh didapati dengan menggabungkan produk antara faktor utama, tetapi untuk menyelesaikan latihan yang dicadangkan, satu -satunya kombinasi yang mencukupi ialah: 432 = 24 × 18 sejak 24 + 18 = 42, kemudian:

x² + 42x + 432 = (x + 24). (x +18)

Rujukan

1. Baldor, a. 1986. Aritmetik teoritis praktikal. Editor syarikat kebudayaan teks Amerika s.Ke.
2. BBC World. Kod alam yang tersembunyi. Diperolehi dari: BBC.com.
3. Dari Leon, Manuel.Nombor Primo: Penjaga Internet. Pulih dari: blog.20 minit.adalah.
4. Unam. Teori Nombor I: Teorem Asas Aritmetik. Diperolehi dari: Theoriarenumeros.Wikidot.com.
5. Wikipedia. Teorem asas aritmetik. Pulih dari: Adakah.Wikipedia.org.