Kerja mekanikal Apa, syarat, contoh, latihan

Dia kerja mekanikal Ia ditakrifkan sebagai perubahan dalam keadaan tenaga sistem, yang disebabkan oleh tindakan daya luaran seperti graviti atau geseran. Unit Kerja Mekanikal dalam Sistem Antarabangsa (SI) adalah Newton X Metro atau Joules, disingkat oleh J.

Secara matematik ia ditakrifkan sebagai produk skalar daya daya oleh anjakan vektor. Yeah F Ia adalah kekuatan yang berterusan dan L Ia adalah anjakan, kedua -dua vektor, kerja w dinyatakan sebagai: W = F ● L

Rajah 1. Walaupun atlet menaikkan berat badan, dia bekerja menentang graviti, tetapi ketika ia mengekalkan berat badan tanpa bergerak, dari sudut pandangan fizik dia tidak melakukan pekerjaan. Sumber: NeedPix.com

Apabila daya tidak malar, maka kita mesti menganalisis kerja yang dilakukan apabila anjakan sangat kecil atau berbeza. Dalam kes ini, jika dianggap sebagai titik permulaan untuk titik A dan sebagai ketibaan di B, jumlah kerja diperoleh dengan menambahkan semua sumbangan yang sama. Ini bersamaan dengan mengira integral berikut:

Dan seperti yang dinyatakan pada mulanya, dengan syarat terdapat perubahan dalam tenaga sistem, ia akan menjadi kerana ada kekuatan dari luar negara yang bertindak di atasnya, oleh itu:

Variasi dalam tenaga sistem = kerja yang dilakukan oleh daya luaran

ΔE = w_ext

Apabila tenaga ditambah ke sistem, w> 0 dan apabila ia ditolak<0. Ahora bien, si ΔE = 0, puede significar que:

-Sistem ini terpencil dan tidak ada daya luaran yang bertindak di atasnya.

-Terdapat kuasa luaran, tetapi mereka tidak melakukan kerja di sistem.

Oleh kerana variasi tenaga bersamaan dengan kerja yang dilakukan oleh daya luaran, unit jika tenaga juga joule. Ini termasuk apa -apa jenis tenaga: kinetik, potensi, termal, kimia dan banyak lagi.

[TOC]

Syarat untuk menjadi kerja mekanikal

Kami telah melihat bahawa kerja itu ditakrifkan sebagai produk skalar. Mari kita ambil definisi kerja yang dilakukan oleh daya berterusan dan gunakan konsep produk skalar antara dua vektor:

W = F ● L = F.L.cos θ

Di mana F Ia adalah magnitud daya, L Ia adalah magnitud anjakan dan θ Ia adalah sudut yang wujud antara daya dan anjakan. Dalam Rajah 2 terdapat contoh daya luaran yang cenderung yang bertindak pada blok (sistem), yang menghasilkan anjakan mendatar.

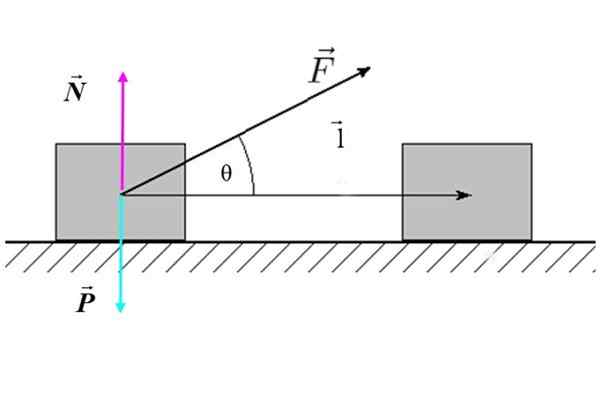Rajah 2. Rajah badan percuma blok yang bergerak di permukaan rata. Sumber: f. Zapata.

Menulis semula kerja seperti berikut:

W = (f. cos θ). L

Kita boleh mengesahkan bahawa hanya komponen daya selari dengan anjakan: F. cos θ emampu melakukan kerja. Jika θ = 90º maka cos θ = 0 dan kerja akan menjadi tidak sah.

Oleh itu disimpulkan bahawa daya tegak lurus untuk anjakan tidak melakukan kerja mekanikal.

Dalam kes Rajah 2, ataupun daya normal N atau berat badan P Mereka bekerja, kerana kedua -duanya berserenjang dengan anjakan L.

Tanda kerja

Seperti yang dijelaskan di atas, W Ia boleh positif atau negatif. Apabila cos θ> 0, Kerja yang dilakukan oleh kekerasan adalah positif, kerana ia mempunyai arah yang sama pergerakan.

Ia boleh melayani anda: Nombor Massa: Apa itu dan Cara mendapatkannya (dengan contoh)

Yeah cos θ = 1, Kekuatan dan anjakan selari dan kerja adalah maksimum.

Dalam kes cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.

Bila cos θ = -1, Kekuatan itu benar -benar bertentangan dengan anjakan, seperti geseran kinetik, yang kesannya adalah untuk menghentikan objek yang bertindak. Jadi kerja adalah minimum.

Ini bersetuju dengan apa yang dikatakan pada mulanya: jika kerja itu positif, tenaga ditambah ke sistem, dan jika ia negatif, ia ditolak.

Kerja bersih W_jaring Ia ditakrifkan sebagai jumlah kerja yang dilakukan oleh semua kuasa yang bertindak pada sistem:

W_jaring = Σw_Yo

Kemudian kita dapat menyimpulkan bahawa untuk menjamin kewujudan kerja mekanikal bersih, perlu:

-Angkatan luaran bertindak ke atas objek.

-Kekuatan ini tidak semua tegak lurus dengan anjakan (cos θ ≠ 0).

-Kerja yang dilakukan oleh setiap daya tidak dibatalkan antara satu sama lain.

-Ada anjakan.

Contoh kerja mekanikal

-Bila -bila masa diperlukan untuk meletakkan objek dalam gerakan berdasarkan rehat, perlu melakukan kerja mekanikal. Contohnya tolak peti sejuk atau batang berat di permukaan mendatar.

-Satu lagi contoh keadaan di mana perlu melakukan kerja mekanikal adalah mengubah kelajuan bola bergerak.

-Perlu melakukan kerja untuk meningkatkan objek pada ketinggian tertentu di lantai.

Sekarang, terdapat situasi yang sama biasa di mana Tidak kerja dilakukan, walaupun penampilan menunjukkan sebaliknya. Kami telah mengatakan bahawa untuk menaikkan objek pada ketinggian tertentu, kita harus melakukan kerja, jadi kita memuatkan objek, kita menaikkannya di atas kepala kita dan menyimpannya di sana. Adakah kita melakukan pekerjaan?

Rupa -rupanya ya, kerana jika objek itu berat, lengan akan menjadi letih tidak lama lagi, bagaimanapun, tidak kira berapa banyak kerja yang dilakukan, kerja tidak dilakukan dari sudut pandang fizik. Kenapa tidak? Kerana objek tidak bergerak.

Satu lagi kes di mana, walaupun mempunyai daya luaran, ia tidak melakukan kerja mekanikal adalah apabila zarah mempunyai pergerakan pekeliling seragam.

Ia boleh melayani anda: usaha biasa: Apa yang terdiri daripada, bagaimana ia dikira, contohnya

Contohnya kanak -kanak yang bertukar batu terikat dengan rentetan. Ketegangan rentetan adalah daya sentripetal yang membolehkan putaran batu. Tetapi pada setiap masa daya ini berserenjang dengan anjakan. Kemudian jangan lakukan kerja mekanikal, walaupun ia nikmat pergerakan.

Kinetik teorem tenaga kerja

Tenaga kinetik sistem adalah apa yang ada di bawah pergerakannya. Yeah m adalah doh dan v Ia adalah kelajuan pergerakan, tenaga kinetik dilambangkan oleh K Dan ia diberikan oleh:

K = ½ mV²

Secara definisi, tenaga kinetik objek tidak boleh negatif, kerana kedua -dua jisim dan kuadrat kelajuan selalu jumlah positif. Tenaga kinetik boleh menjadi 0, ketika objek sedang berehat.

Untuk menukar tenaga kinetik sistem, perlu-. Untuk ini, perlu melakukan kerja bersih pada sistem, oleh itu:

W_jaring = ΔK

Ini adalah teorem kerja - tenaga kinetik. Menyatakan bahawa:

Kerja bersih bersamaan dengan perubahan tenaga kinetik sistem

Perhatikan bahawa walaupun k sentiasa positif, ΔK boleh positif atau negatif, kerana:

ΔK = k_final - K _permulaan

Yeah K_final >K _permulaan Sistem telah mendapat tenaga dan ΔK> 0. Sebaliknya, ya K_final < K _permulaan, Sistem telah menghasilkan tenaga.

Kerja yang dilakukan untuk meregangkan musim bunga

Semasa meregangkan (atau memampatkan) musim bunga, perlu melakukan pekerjaan. Kerja ini disimpan pada musim bunga, membolehkan ini seterusnya berfungsi, katakan, blok yang dilampirkan pada salah satu hujungnya.

Undang -undang Hooke menyatakan bahawa kekuatan yang dikenakan oleh musim bunga adalah kekuatan pengembalian - ia bertentangan dengan anjakan - dan juga berkadar dengan anjakan tersebut. Pemalar perkadaran bergantung pada bagaimana musim bunga adalah: lembut dan mudah cacat atau tegar.

Kekuatan ini diberikan oleh:

F_r = -kx

Dalam ungkapan, F_r Ia adalah kekuatan, k Ia adalah pemalar musim bunga dan x Ia adalah anjakan. Tanda negatif menunjukkan bahawa daya yang dikenakan oleh musim bunga menentang anjakan.

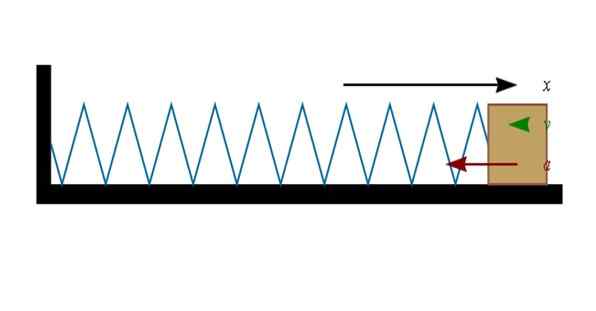Rajah 3. Musim bunga yang dimampatkan atau diregangkan berfungsi pada objek yang diikat pada akhir. Sumber: Wikimedia Commons.

Sekiranya musim bunga dimampatkan (ke kiri dalam angka), blok pada akhirnya akan bergerak ke kanan. Dan apabila musim bunga diregangkan (kanan) blok akan mahu bergerak ke kiri.

Untuk memampatkan atau meregangkan musim bunga, sesetengah ejen luaran mesti melakukan pekerjaan itu, dan kerana ia adalah daya berubah, untuk mengira kerja ini, anda perlu menggunakan definisi yang berlaku pada mulanya:

Boleh melayani anda: undang -undang darcy

Sangat penting untuk diperhatikan bahawa ini adalah kerja yang dilakukan oleh ejen luaran (tangan seseorang, sebagai contoh) untuk memampatkan atau meregangkan musim bunga. Itulah sebabnya tanda negatif tidak muncul. Dan sebagai jawatan adalah persegi, tidak kira sama ada mereka adalah pemampatan atau pemanjangan.

Kerja yang akan melakukan musim bunga pada gilirannya adalah:

W_Spring = -W_ext

Latihan

Latihan 1

Blok dalam Rajah 4 mempunyai jisim m = 2 kg dan tergelincir melalui satah cenderung tanpa geseran, dengan α = 36.Ke -9. Dengan mengandaikan bahawa ia dibenarkan untuk tergelincir dari selebihnya dari bahagian atas pesawat, yang ketinggiannya adalah h = 3 m, cari kelajuan yang blok mencapai pangkalan pesawat, melalui kinetik tenaga tenaga kerja tenaga kerja.

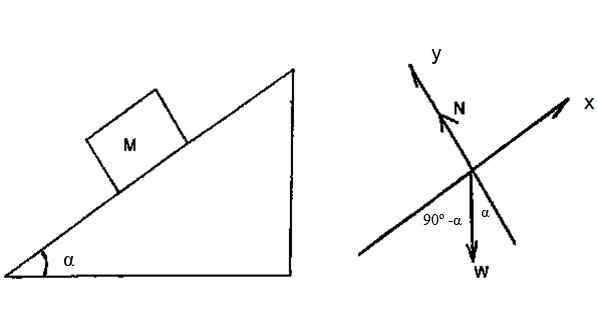Rajah 4. Blok slaid ke atas satah cenderung tanpa menggosok. Sumber: f. Zapata.

Penyelesaian

Rajah badan bebas menunjukkan bahawa satu -satunya daya yang mampu melakukan kerja di blok adalah berat badan. Lebih tepat: komponen berat di sepanjang paksi x.

Jarak yang dilalui oleh blok di atas kapal terbang dikira oleh trigonometri:

D = 3 / (cos 36.9º) m = 3.75 m

W_berat = (Mg). d. cos (90-α) = 2 x 9.8 x 3.75 x cos 53.J = 44.1 j

Dengan bekerja kinetik tenaga teorem:

W_jaring = ΔK

W_jaring = W_berat

ΔK = ½ mV_F²- ½ mV_{Sama ada}²

Kerana ia dibebaskan dari rehat, v_{Sama ada} = 0, Oleh itu:

W_jaring = ½ mV_F²

Latihan 2

Musim bunga mendatar, yang pemalarnya adalah k = 750 n/m ditetapkan oleh satu hujung ke dinding. Satu orang memampatkan hujung yang lain jarak 5 cm. Hitung: a) Daya yang dikenakan oleh orang itu, b) kerja yang dilakukannya untuk memampatkan musim bunga.

Penyelesaian

a) Besarnya daya yang digunakan oleh orang itu adalah:

F = kx = 750 n/ m . 5 x 10 ^-2 M = 37.5 n.

b) Sekiranya hujung musim bunga pada asalnya berada di x₁ = 0, untuk membawanya dari sana ke kedudukan akhir x₂ = 5 cm, perlu melakukan kerja berikut, mengikut hasil yang diperolehi di bahagian sebelumnya:

W_ext = ½ k (x₂² - x₁²) = 0.5 x 750 x (0.05² -0²) J = 0.9375 J.

Rujukan

1. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 2. Dinamik. Diedit oleh Douglas Figueroa (USB).
2. Iparraguirre, l. 2009. Mekanik asas. Koleksi Sains Semula Jadi dan Matematik. Pengagihan dalam talian percuma.
3. Knight, r. 2017. Fizik untuk saintis dan kejuruteraan: Pendekatan Strategi. Pearson.
4. Fizik Libretxts. Teorem tenaga kerja. Pulih dari: Phys.Libretxts.org
5. Kerja dan tenaga. Pulih dari: fizik.Bu.Edu
6. Kerja, tenaga dan kuasa. Pulih dari: ncert.Nic.dalam