Fourier Transform Properties, Aplikasi, Contoh

The Transformasi Fourier Ini adalah kaedah kecukupan analisis yang berorientasikan kepada fungsi integrasi yang dimiliki oleh keluarga tKomprehensif Ransformed. Ia terdiri daripada fungsi semula fungsi F (t) Dari segi kos (t) dan sen (t).

Identiti trigonometri fungsi -fungsi ini, bersama -sama dengan ciri -ciri derivasi dan antiderivasi mereka, berfungsi untuk menentukan perubahan Fourier melalui fungsi kompleks berikut:

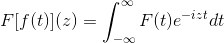
Yang dipenuhi sementara ungkapan itu masuk akal, iaitu, apabila integral yang tidak wajar adalah konvergen. Secara algebra dikatakan bahawa transformasi Fourier adalah homeomorfisme linear.

Sebarang fungsi yang boleh dilakukan dengan transformasi Fourier mesti membentangkan pembatalan di luar parameter yang ditetapkan.

[TOC]

Sifat

Sumber: Pexels

Transformasi Fourier memenuhi sifat berikut:

Kewujudan

Untuk mengesahkan kewujudan transformasi Fourier menjadi fungsi f (t) yang ditakrifkan dalam Royals R, 2 aksioma berikut mesti dipenuhi:

1. f (t) berterusan untuk semua untuk semuanya R
2. f (t) boleh dimengerti R

Linearity Transformasi Fourier

Biarkan m (t) dan n (t) dua fungsi dengan fourier ditakrifkan, dengan pemalar a dan b ada.

F [a m (t) + b n (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)

Yang juga bergantung pada linearity yang integral dengan nama yang sama.

Fourier berubah dari derivatif

Anda mempunyai fungsi F  yang berterusan dan terintegrasi dalam semua reais, di mana:

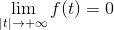
Dan terbitan F (f ') Ia berterusan dan ditakrifkan dalam semua perkara R

Transformasi Fourier dari derivatif ditakrifkan oleh integrasi oleh bahagian, dengan ungkapan berikut:

F [f '(t)] (z) = izF [f (t)] (z)

Dalam derivasi pesanan yang lebih tinggi, ia akan digunakan secara homolog, di mana untuk semua n 1 anda perlu:

F [f ⁿ'(t)] (z) = (iz)ⁿF [f (t)] (z)

Pembezaan transformasi Fourier

Anda mempunyai fungsi F  yang berterusan dan terintegrasi dalam semua reais, di mana:

I (d/dz)F [f (t)] (z) = F  [t .  f (t)] (z)

Fourier berubah dari terjemahan

Untuk semua θ yang dimiliki oleh satu set dan T Itu milik set s ', anda mesti:

F [ τ_ke θ] =  dan^-Iay F [ θ]                                 F [ τ_keT ] =  dan^-Iax  F [ T]   

Dengan  τ_ke  bekerja sebagai pengendali terjemahan di vektor ke.

Terjemahan transformasi Fourier

Untuk semua θ yang dimiliki oleh satu set dan T Itu milik set s ', anda mesti:

τ_ke F [θ] =  F [Dan^-Iax.θ]                                τ_ke F [t ] =  F [Dan^-Iay . T]

Boleh melayani anda: hypercubo: definisi, dimensi, koordinat, terungkap

Untuk semua ke yang dimiliki R

Fourier Transform kumpulan skala

Untuk semua θ yang dimiliki oleh set s. T yang milik set s '

λ kepunyaan R - 0  Kamu perlu:

F [θ (λx)] = (1 / | λ |) F [θ] (dan/λ)                 

F [T (λx)] = (1 / | λ |) F [T] (dan/λ)

Yeah F Ia adalah fungsi yang berterusan dan semata -mata, di mana> 0. Jadi:

F [f (at)] (z) =   (1/a) F [f (t)] (z/a) 

Untuk menunjukkan hasil ini, kita dapat meneruskan perubahan pembolehubah.

Bila t → + kemudian s = pada → + ∞

Bila t → - kemudian s = pada → - ∞

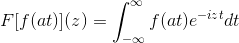
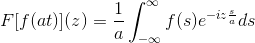
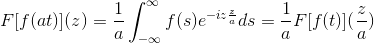
Simetri

Untuk mengkaji simetri transforma Fourier.

Anda mempunyai θ dan δ yang tergolong dalam S. Dari sana ia dapat disimpulkan bahawa:

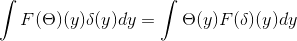
Memperoleh

1 / (2π)^d  F [θ ], F [δ] Identiti parseval

1 / (2π)^D/2  || F [θ ] ||_L²_R^d     Formula Plancherel

Fourier berubah dari produk menjadi konvolusi

Mengejar objektif yang sama yang dalam perubahan Laplace, konvolusi fungsi merujuk kepada produk di antara Fourier Transforms.

Ia mempunyai f dan g sebagai 2 fungsi terhad, ditakrifkan dan sepenuhnya berintegrasi:

F (f *g) = f (f) . F (g)

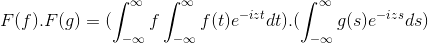
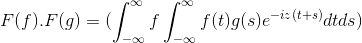
Kemudian ketika membuat perubahan pemboleh ubah

t + s = x; Integral ganda integral berganda diteruskan

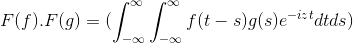
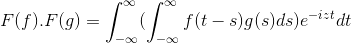
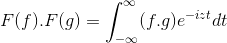
F (f) . F (g) = f (f . g)

Kesinambungan dan jatuh di tak terhingga

Untuk semua θ yang dimiliki oleh R, f [ θ] mematuhi kriteria fungsi berterusan terhad dalam r^d.

Juga F [ θ] (y) → 0 dalam c si | y | → ∞

Sejarah

Konsep matematik ini disampaikan oleh Joseph B. Fourier pada tahun 1811 ketika membangunkan perjanjian mengenai Penyebaran haba. Ia dengan cepat diterima oleh pelbagai cabang sains dan kejuruteraan.

Ia ditubuhkan sebagai alat kerja utama dalam kajian persamaan dengan derivatif separa, membandingkan walaupun dengan hubungan kerja antara Laplace berubah dan persamaan pembezaan biasa.

Apakah transformasi Fourier untuk?

Ia berfungsi terutamanya kepada persamaan yang signifikan, sambil mengubah ekspresi yang diperolehi menjadi elemen kuasa, yang menunjukkan ungkapan pembezaan dalam bentuk polinomial bersepadu.

Dalam pengoptimuman, modulasi dan pemodelan hasil ia bertindak sebagai ungkapan piawai, menjadi sumber yang kerap untuk kejuruteraan selepas beberapa generasi.

Siri Fourier

Mereka ditakrifkan siri dari segi cosen dan payudara; Mereka berkhidmat untuk memudahkan kerja dengan fungsi berkala umum. Apabila digunakan, mereka adalah sebahagian daripada teknik penyelesaian persamaan pembezaan separa dan biasa.

Ia dapat melayani anda: fungsi pembolehubah sebenar dan perwakilan grafiknya

Siri Fourier lebih umum daripada siri Taylor, kerana mereka membangunkan fungsi Discontinua berkala yang tidak mempunyai perwakilan dalam siri Taylor.

Bentuk lain dalam siri Fourier

Untuk secara analitik memahami perubahan Fourier, ia penting.

-Siri Fourier pada fungsi tempoh 2L

Ramai kali perlu menyesuaikan struktur siri Fourier, ke fungsi berkala yang tempohnya P = 2L> 0 dalam selang [-L, L].

-Siri Fourier dalam fungsi Even dan Ganjil

Selang [-π, π] dianggap yang menawarkan kelebihan apabila memanfaatkan ciri-ciri simetri fungsi.

Sekiranya F adalah tork Siri Fourier ditubuhkan sebagai satu siri Cosenos.

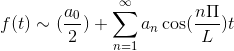
Sekiranya F adalah ganjil, siri Fourier ditubuhkan sebagai satu siri payudara.

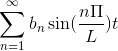
-Notasi kompleks siri Fourier

Jika anda mempunyai fungsi F (t), yang memenuhi semua keperluan maju siri Fourier, adalah mungkin untuk menunjukkannya dalam selang [-t, t] menggunakan notasi kompleksnya:

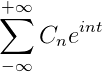
Aplikasi

Sumber: Pexels

Pengiraan penyelesaian asas

Transformasi Fourier adalah alat yang berkuasa dalam kajian persamaan pembezaan separa jenis linear dengan pekali tetap. Memohon fungsi dengan domain tidak terhad sama rata.

Seperti transformasi Laplace, transformasi Fourier mengubah fungsi derivatif separa, menjadi persamaan pembezaan biasa lebih mudah untuk beroperasi.

Masalah Cauchy untuk persamaan haba membentangkan medan kerap aplikasi transformasi Fourier di mana fungsi dijana Dirichlet panas atau nukleus teras.

Mengenai pengiraan penyelesaian asas, kes -kes berikut dibentangkan di mana ia adalah perkara biasa untuk mencari transformasi Fourier:

-Persamaan Laplace

-Persamaan haba

-Persamaan Schrödinger

-Persamaan Gelombang

Teori isyarat

Alasan umum untuk penerapan transformasi Fourier di cawangan ini kebanyakannya disebabkan oleh penguraian ciri isyarat sebagai pertindihan tak terhingga dari isyarat yang lebih mudah dirawat.

Ia boleh menjadi gelombang bunyi atau gelombang elektromagnet, transformasi Fourier mengekspresikannya dalam gelombang mudah bertindih. Perwakilan ini agak kerap dalam kejuruteraan elektrik.

Boleh melayani anda: garis menegak

Sebaliknya, mereka adalah contoh penggunaan transformasi Fourier dalam bidang teori isyarat:

-Masalah pengenalan sistem. Ditubuhkan f dan g

-Masalah dengan konsistensi isyarat output

-Masalah dengan penapisan isyarat

Contoh

Contoh 1

Tentukan transformasi Fourier untuk ungkapan berikut:

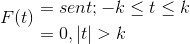
Kita juga boleh mewakilinya seperti berikut:

F (t) = Dosa (t) [h_{(T + k)} - H_{(T - k)} ]

Nadi segi empat tepat ditakrifkan:

p (t) = h_{(T + k)} - H_{(T - k)}

Transformasi Fourier digunakan untuk ungkapan seterusnya yang menyerupai teorem modulasi.

f (t) = p (t) dosa (t)

Di mana: F [w] = (1/2) i [p (w + 1) - p (w - 1)]

Dan transformasi Fourier ditakrifkan oleh:

F [w] =  (1/2) i [(2/2w+1) Sen (k (w+1)) - (2/2w+1) Sen (k (w-1))]

Contoh 2

Tentukan transformasi Fourier untuk ekspresi:

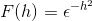Dengan definisi kita menyatakan perubahan seperti berikut

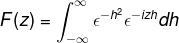
Kerana f (h) adalah fungsi yang lebih baik, ia boleh ditegaskan bahawa

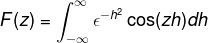Memperoleh dalam integral berkenaan dengan z, ungkapan boleh ditulis semula. Langkah ini penting dalam kerja dengan persamaan pembezaan.

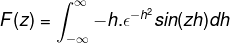
Integrasi mengikut bahagian digunakan dengan memilih pembolehubah dan perbezaannya seperti berikut

u = dosa (zh) du = z cos (zh) dh

dv = h (e^-h)²                       V = (e^-h)² / 2

Menggantikannya

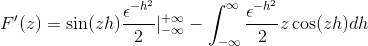
Setelah menilai di bawah teorem asas pengiraan

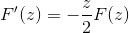
Memohon pengetahuan terdahulu yang berkaitan dengan persamaan pembezaan urutan pertama, ungkapan itu dilambangkan sebagai

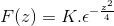
Untuk mendapatkan k kita menilai 

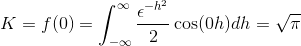
Akhirnya, perubahan Fourier ditakrifkan sebagai

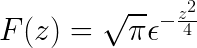
Latihan yang dicadangkan

• Tentukan ungkapan Fourier Expression
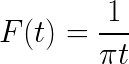
• Selesaikan integral yang tidak wajar berikut menggunakan persamaan Pareseval
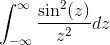
• Dapatkan transformasi ungkapan w/(1+w²)

Rujukan

1. Duoandikoetxea Zuazo, J., Analisis Fourier. Addison- Wesley Iberoamericana, Universiti Autonomi Madrid, 1995.
2. Singa, j. L., Analisis matematik dan kaedah berangka untuk sains dan teknologi. Springer-Verlag, 1990.
3. Lieb, e. H., Kernel Gaussian hanya mempunyai Gaussian Maximizers. Mencipta. Matematik. 102, 179-208, 1990.
4. Dym, h., McKean, h. P., Siri Fourier dan Integral. Akademik Akhbar, New York, 1972.
5. Schwartz, l., Théorie des Distributions. Ed. Hermann, Paris, 1966.