Escaleno Trapezio Properties, Formula dan Persamaan, Contoh

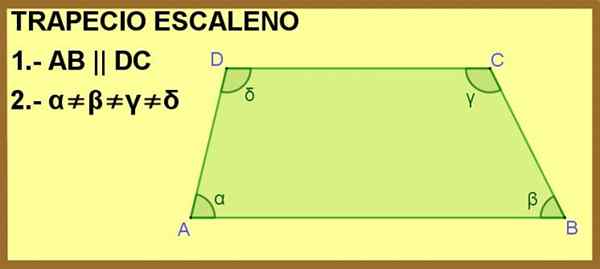
A trapeze scalene Ia adalah poligon empat yang berpandu, dua daripadanya selari antara satu sama lain, dan dengan empat sudut dalamannya yang berbeza.

Duadrilateral ABCD ditunjukkan, di mana sisi AB dan DC selari antara satu sama lain. Dengan ini, sudah cukup untuk menjadikannya trapeze, tetapi di samping itu, sudut dalaman α, β, γ dan δ adalah berbeza, oleh itu trapezoid adalah eskalano.

Rajah 1. Quadrilateral ABCD adalah trapeze untuk keadaan 1 dan scalene untuk keadaan 2. Sumber: f. Zapata.

[TOC]

Unsur -unsur Scaleno Trapect

Di bawah elemen yang paling ciri:

-Pangkalan dan sisi: Sisi selari trapezoid adalah pangkalannya dan kedua -dua sisi bukan selalunya adalah sisi.

Dalam trapezio scalene, pangkalannya adalah panjang yang berbeza dan sisi juga. Walau bagaimanapun, trapezoid scalene boleh mempunyai sisi panjang yang sama sebagai asas.

-Median: Ia adalah segmen yang bergabung dengan titik tengah di sisi.

-Pepenjuru: Diagonal trapeze adalah segmen yang bergabung dengan dua titik bertentangan. Trapeze, seperti setiap segi empat, mempunyai dua pepenjuru. Dalam trapezio scalene mereka mempunyai panjang yang berbeza.

Trapezoid lain

Sebagai tambahan kepada trapezio Escaleno, terdapat trapezoid tertentu: trapezoid segi empat tepat dan trapezoid isosceles.

Trapeze adalah segi empat tepat apabila salah satu sudutnya lurus, sementara trapezio isosceles mempunyai sisi panjang yang sama.

Bentuk trapezoid mempunyai banyak aplikasi di peringkat reka bentuk dan industri, seperti dalam konfigurasi sayap pesawat, bentuk objek sehari -hari seperti jadual, sandaran kerusi, bekas, dompet, cetakan tekstil dan banyak lagi.

Rajah 2. Bentuk trapezoid adalah biasa dalam konfigurasi pesawat Alar. Sumber: Wikimedia Commons.

Sifat

Seterusnya, sifat trapezoid memanjat disenaraikan, yang kebanyakannya luas dengan jenis trapezoid yang lain. Dalam apa yang berikut, apabila anda bercakap tentang "trapezio", harta itu akan terpakai kepada apa -apa jenis, termasuk scalene.

1. Median trapezoid, iaitu segmen yang menyatukan titik pertengahan dari sisi bukan selari, selari dengan mana -mana pangkalan.

2.- Median trapezoid mempunyai panjang yang separa dari pangkalannya dan memotong pepenjuru di tengah titik.

3.- Diagonal trapeze bersilang pada titik yang membahagikannya kepada dua bahagian yang berkadar dengan nisbah pangkalan.

4.- Jumlah dataran pepenjuru trapeze adalah sama dengan jumlah kuadrat di sisi ditambah produk ganda pangkalannya.

5.- Segmen yang menyertai titik pertengahan -diagonal mempunyai panjang sama dengan separuh -penularan pangkalan.

Boleh melayani anda: fungsi injective: apa yang terdiri daripada, apa itu dan contohnya

6.- Sudut bersebelahan dengan sisi adalah tambahan.

7.- Dalam trapeze scalene panjang pepenjuru adalah berbeza.

8.- Trapeze mempunyai lilitan berdaftar hanya jika jumlah pangkalannya sama dengan jumlah sisinya.

9.- Sekiranya trapeze mempunyai lilitan berdaftar, maka sudut dengan puncak di tengah lilitan dan sisi yang melewati hujung sisi trapeze adalah lurus.

10.- Trapeze Escaleno tidak mempunyai lilitan yang dibentangkan, satu -satunya jenis trapeze yang jika ia adalah isosceles.

Formula dan persamaan

Hubungan berikut trapeze memanjat dirujuk kepada angka berikut.

1.- Jika Ae = ed dan Bf = Fc → EF || AB dan EF || DC.

2.- Ef = (ab + dc)/2 iaitu: m = (a + c)/2.

3.- DI = IB = D₁ /2 dan ag = gc = d₂ /2.

4.- DJ / JB = (c / a) Begitu juga CJ / JA = (C / A).

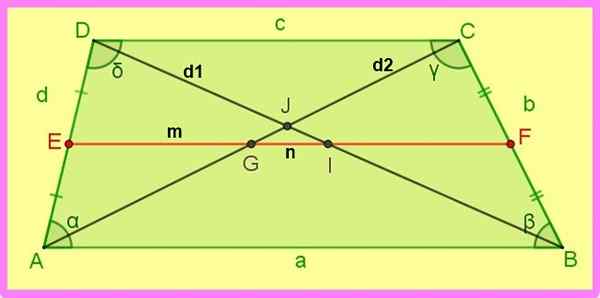Rajah 3. Median dan pepenjuru trapezoid scalene. Sumber: f. Zapata.

5.- Db² + Ac² = AD² + BC² + 2 ab ∙ dc 

Sama sekali:

d₁² + d₂² = d² + b² + 2 a ∙ c

6.- Gi = (ab - dc)/2

Iaitu:

n = (a - c)/2

7.- α + δ = 180⁰ dan β + γ = 180⁰

8.- Jika α ≠ β ≠ γ δ δ maka d1 ≠ d2.

9.- Rajah 4 menunjukkan trapezoid scalene yang mempunyai lilitan berdaftar, dalam hal ini dipenuhi:

A + C = D + B

10.- Dalam trapezoid ABCD Escalene dengan pusat berdaftar pusat atau yang berikut juga dipenuhi:

∡aod = ∡boc = 90⁰

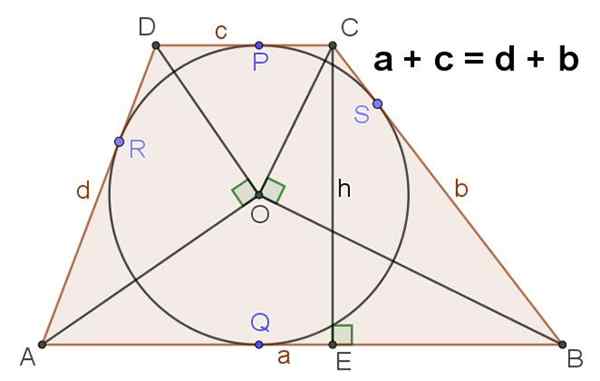Rajah 4. Sekiranya dalam trapeze ia disahkan bahawa jumlah pangkalannya sama dengan jumlah sisi, maka ada lilitan yang ditulis dalam hal yang sama. Sumber: f. Zapata.

Ketinggian

Ketinggian trapeze ditakrifkan sebagai segmen yang berjalan dari titik asas secara serentak ke pangkalan yang bertentangan (atau lanjutannya).

Semua ketinggian trapeze mempunyai ukuran yang sama H, jadi kebanyakan masa ketinggian perkataan merujuk kepada pengukurannya. Singkatnya, ketinggian adalah jarak atau pemisahan antara pangkalan.

Ketinggian H dapat ditentukan jika panjang sisi dan salah satu sudut bersebelahan dengan sisi diketahui:

H = d sin (α) = d sin (γ) = b sin (β) = b sin (δ)

Median

Ukuran median trapezoid adalah separa -bodi pangkalan:

M = (a + b)/2

Diagonal

d₁ = √ [a² + d² - 2 ∙ A ∙ D ∙ cos (α)]

d₂= √ [a² + b² - 2 ∙ A ∙ B ∙ cos (β)]

Ia juga boleh dikira jika hanya panjang trapezoid yang diketahui:

d₁ = √ [b² + A ∙ C - A (B² - d²)/(a - c)]

d₂ = √ [D² + A ∙ C - A (D² - b²)/(a - c)]

Perimeter

Perimeter adalah jumlah panjang kontur, iaitu, jumlah semua sisinya:

Boleh melayani anda: Pemboleh ubah rawak diskret

P = a + b + c + d

Kawasan

Kawasan trapezoid adalah separa -bodi pangkalannya yang didarab dengan ketinggiannya:

A = h ∙ (a + b)/2

Ia juga boleh dikira jika median m dan ketinggian diketahui:

A = m ∙ h

Sekiranya hanya panjang sisi trapezoid yang diketahui, kawasan ini dapat ditentukan oleh formula Herón untuk trapezoid:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]

Di mana s adalah separuh -perekatan: s = (a+b+c+d)/2.

Hubungan lain untuk pendakian mendaki

Potongan median dengan pepenjuru dan selari yang melalui persimpangan pepenjuru, menimbulkan hubungan lain.

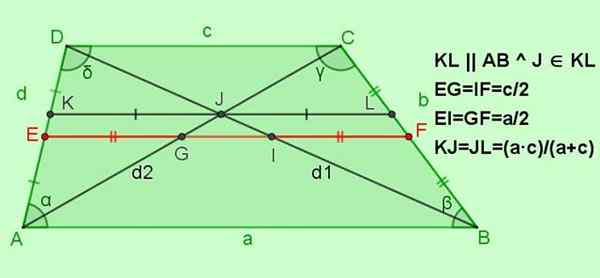Rajah 5. Hubungan lain untuk pendakian mendaki. Sumber: f. Zapata.

-Hubungan untuk median ef

Ef = (a+c)/2; Eg = jika = c/2; Ei = gf = a/2

-Hubungan untuk segmen selari ke pangkalan KL, dan yang melewati titik Persimpangan j dari pepenjuru

Ya KL || AB || DC dengan j ∈ Kl, kemudian kJ = jl = (a ∙ c)/(a+c)

Pembinaan trapezium scalene dengan peraturan dan kompas

Diberi pangkalan panjang ke dan c, menjadi> c dan dengan panjang panjang b dan d, menjadi b> d, Kami meneruskan langkah -langkah ini (lihat Rajah 6):

1.- Dengan peraturan segmen AB terbesar ditarik.

2.- Dari se dan di ab, titik p ditandakan supaya ap = c.

3.- Dengan kompas dengan C dan Radio D Center, arka ditarik.

4.- Ia dibuat pusat di B dengan radio B melukis arka yang menafsirkan arka yang dibuat pada langkah sebelumnya. Kami menyebut bahawa titik persimpangan.

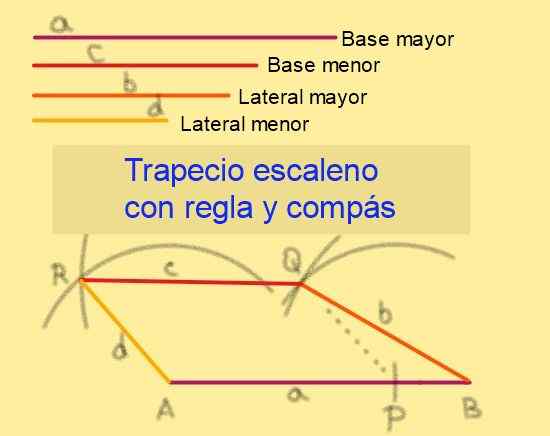Rajah 6. Pembinaan Escaleno Trapecio diberikan sisinya. Sumber: f. Zapata.

5.- Dengan pusat dalam melukis arka radius d.

6.- Dengan pusat di mana untuk menarik arka jejari yang dipintas dengan arka yang disediakan dalam langkah sebelumnya. Ia akan dipanggil r ke titik pemotongan.

7.- Segmen BQ, QR dan RA ditarik dengan peraturan.

8.- Quadrilateral ABQR adalah trapezoid scalene, kerana APQR adalah paralelogram, yang menjamin bahawa AB || Q.

Contoh

Panjang berikut diberikan dalam cm: 7, 3, 4 dan 6.

a) Tentukan sama ada dengan mereka, anda boleh membina trapeze scalene yang boleh dilampirkan ke lilitan.

b) Cari perimeter, kawasan, panjang pepenjuru dan ketinggian trapeze tersebut, serta jejari lilitan berdaftar.

- Penyelesaian kepada

Menggunakan segmen panjang 7 dan 3 sebagai pangkalan dan panjang 4 dan 6 sebagai sisi, trapezoid scalene boleh dibina menggunakan prosedur yang diterangkan di bahagian sebelumnya.

Kita perlu menyemak sama ada ia mempunyai lilitan yang berdaftar, tetapi mengingati harta (9):

Boleh melayani anda: prisma heksagon

Trapeze mempunyai lilitan berdaftar hanya jika jumlah pangkalannya sama dengan jumlah sisinya.

Kami melihatnya memang:

7 + 3 = 4 + 6 = 10

Maka keadaan lilitan yang ditulis dipenuhi.

- Penyelesaian b

Perimeter

Perimeter p diperoleh dengan menambahkan sisi. Oleh kerana pangkalan keseluruhan 10 dan sisi juga, perimeter adalah:

P = 20 cm

Kawasan

Untuk menentukan kawasan itu, hanya diketahui oleh sisinya, hubungannya digunakan:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]

Di mana s adalah separuh -perekatan:

S = (a+b+c+d)/2.

Dalam kes kita, separuh -perekatan bernilai s = 10 cm. Setelah menggantikan nilai masing -masing:

A = 7 cm; B = 6 cm; C = 3 cm; D = 4 cm

Ditinggalkan:

A = [10/4] √ [(3) (7) (-1) (-3)] = (5/2) √63 = 19,84 cm².

Ketinggian

Ketinggian H berkaitan dengan kawasan A melalui ungkapan berikut:

A = (A+C) ∙ H/2, di mana ketinggian boleh diperolehi dengan pelepasan:

H = 2a / (a+c) = 2 * 19.84 / 10 = 3,968 cm.

Radio lilitan berdaftar

Radius lilitan berdaftar bernilai separuh daripada ketinggian:

R = H/2 = 1,984 cm

Diagonal

Akhirnya ada panjang pepenjuru:

d₁ = √ [b² + A ∙ C - A (B² - d²)/(a - c)]

d₂ = √ [D² + A ∙ C - A (D² - b²)/(a - c)]

Menggantikan nilai dengan betul adalah:

d₁ = √ [6² + 7 ∙ 3 - 7 (6² - 4²)/(7 - 3)] = √ (36+21-7 (20)/4) = √ (22)

d₂ = √ [4² + 7 ∙ 3 - 7 (4² - 6²)/(7-3)] = √ (16+21-7 (-20)/4) = √ (72)

Iaitu: D₁ = 4.69 cm dan d₂ = 8.49 cm

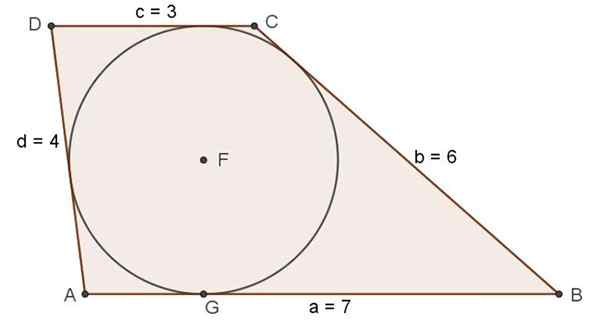Rajah 7. Scalene trapezio yang memenuhi syarat kewujudan lilitan berdaftar. Sumber: f. Zapata.

Latihan diselesaikan

Tentukan sudut dalaman trapezoid asas ab = a = 7, cd = c = 3 dan lateral bc = b = 6, da = d = 4.

Penyelesaian

Teorem Cosine boleh digunakan untuk menentukan sudut. Contohnya, sudut ∠A = α ditentukan dari segitiga abd dengan ab = a = 7, bd = d2 = 8.49 dan da = d = 4.

Teorem Cosine yang digunakan untuk segitiga ini tetap seperti ini:

d₂² = a² + d² - 2 ∙ a ∙ d ∙ cos (α), iaitu:

72 = 49+16-56 ∙ cos (α).

Apabila membersihkan, kosinus sudut α diperoleh:

Cos (α) = -1/8

Iaitu α = arccos (-1/8) = 97.18⁰.

Dengan cara yang sama sudut lain diperoleh, sebagai nilai mereka:

β = 41.41⁰; γ = 138.59⁰ dan akhirnya δ = 82.82⁰.

Rujukan

1. C. Dan. Ke. (2003). Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universiti Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematik 2. Kumpulan Editorial Patria.
3. Dibebaskan, k. (2007). Cari poligon. Syarikat Pendidikan Benchmark.
4. Hendrik, v. (2013). Poligon umum. Birkhäuser.
5. Iger. (s.F.). Matematik semester pertama Tacaná. Iger.
6. Jr. Geometri. (2014). Poligon. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Matematik: Penalaran dan Aplikasi (Edisi Kesepuluh). Pendidikan Pearson.
8. Patiño, m. (2006). Matematik 5. Progreso editorial.
9. Wikipedia. Trapeze. Pulih dari: Adakah.Wikipedia.com