Sejarah segitiga, elemen, klasifikasi, sifat

The segitiga Mereka adalah angka geometri yang rata dan tertutup, yang terdiri daripada tiga sisi. Segitiga ditentukan oleh tiga baris yang dipotong dua hingga dua, membentuk antara satu sama lain tiga sudut. Bentuk segi tiga, penuh simbolisme, hadir dalam objek yang tak terhitung jumlahnya dan sebagai elemen pembinaan.

Asal segitiga hilang dalam sejarah. Dari bukti arkeologi diketahui bahawa kemanusiaan primitif mengenalnya dengan baik, kerana sisa arkeologi mengesahkan bahawa dia digunakan dalam alat dan senjata.

Rajah 1. Segitiga. Sumber: Domainpartures awam.

Juga jelas bahawa orang Mesir kuno mempunyai pengetahuan yang kukuh tentang geometri dan khususnya bentuk segi tiga. Mereka terkandung dalam unsur -unsur seni bina pembinaan monumental mereka.

Di papirus Rhind terdapat formula untuk pengiraan segitiga dan kawasan trapeze, serta beberapa jilid dan konsep lain tentang trigonometri asas.

Sebaliknya, diketahui bahawa orang Babilon dapat mengira kawasan segitiga dan angka geometri lain, yang mereka gunakan untuk tujuan praktikal, seperti bahagian tanah. Mereka juga menyedari banyak sifat segitiga.

Walau bagaimanapun, ia adalah orang Yunani kuno yang sistematik banyak konsep geometri yang kerap hari ini, walaupun banyak pengetahuan itu tidak eksklusif, kerana ia pasti dikongsi dengan tamadun kuno yang lain.

[TOC]

Unsur -unsur segitiga

Unsur -unsur segitiga mana -mana ditunjukkan dalam angka berikut. Terdapat tiga: simpang, sisi dan sudut.

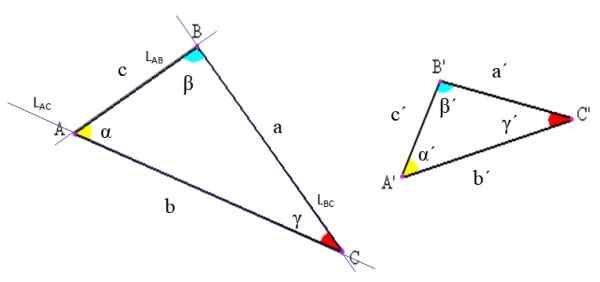Rajah 2. Notasi segitiga dan unsur mereka. Sumber: Wikimedia Commons, diubahsuai oleh F. Zapata

-Simpang: Ini adalah titik persimpangan garisan yang segmennya menentukan segitiga. Dalam angka atas sebagai contoh, garis l_Ac yang mengandungi segmen AC, memotong garis l_Ab yang mengandungi segmen ab pada titik a.

-Sisi: Antara setiap beberapa simpang segmen garis ditarik yang merupakan satu sisi segitiga. Segmen ini boleh dilambangkan dengan huruf hujung atau menggunakan surat tertentu untuk memanggilnya. Dalam contoh Rajah 2, sisi ab juga dipanggil "C".

-Sudut: Di antara setiap sisi dengan puncak biasa sudut berasal, yang puncaknya bertepatan dengan segitiga. Sudut biasanya dilambangkan dengan surat Yunani, seperti yang dinyatakan pada awalnya.

Untuk membina segitiga tertentu, dengan bentuk dan saiz tertentu, hanya mempunyai beberapa set data berikut:

-Tiga sisi, agak jelas dalam kes segitiga.

-Dua sisi dan sudut di antara mereka, dan bahagian yang tersisa segera ditarik.

-Dua sudut (dalaman) dan sisi antara mereka. Dengan lanjutan, kedua -dua pihak yang hilang ditarik dan segitiga sudah siap.

Notasi

Umumnya dalam notasi segitiga konvensyen berikut digunakan: simpang ditunjukkan dengan huruf besar, sisi dengan huruf Latin kecil dan sudut dengan huruf Yunani (lihat Rajah 2).

Dengan cara ini segitiga dinamakan mengikut simpulnya. Sebagai contoh, segitiga di sebelah kiri dalam Rajah 2 adalah segitiga ABC, dan yang di sebelah kanan adalah segitiga A'b'c '.

Ia juga mungkin menggunakan notasi lain; Sebagai contoh, sudut α dalam Rajah 2 dilambangkan sebagai BAC. Perhatikan bahawa huruf puncak masuk di tengah dan huruf ditulis dalam arah yang bertentangan dengan jarum jam.

Ia dapat melayani anda: perselisihan masalah

Lain kali aksen circumflex diletakkan untuk menunjukkan sudut:

Atau simbol ∠ digunakan, kerana notasi sebelumnya mungkin tidak mudah dicetak, diikuti dengan huruf yang sepadan dengan puncak:

α = ∠A

Jenis segitiga

Terdapat beberapa kriteria klasifikasi segitiga. Yang paling biasa adalah untuk mengklasifikasikannya mengikut ukuran sisi mereka atau mengikut ukuran sudut mereka. Bergantung pada ukuran sisi mereka, segitiga boleh: scalenes, isosceles atau equilaterals:

-Scalene: Ketiga -tiga pihaknya berbeza.

-Isosceles: Ia mempunyai dua sisi yang berbeza dan satu.

-Sama: Ketiga -tiga pihak adalah sama.

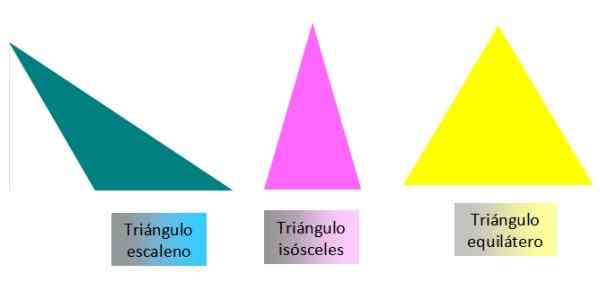Rajah 3. Klasifikasi segitiga di sisi mereka. Sumber: f. Zapata

Mengikut ukuran sudut mereka, segitiga dipanggil seperti ini:

-Bodoh, Sekiranya salah satu sudut dalaman lebih besar daripada 90º.

-Acutangle, Apabila tiga sudut dalaman segitiga akut, iaitu, kurang daripada 90º

-Rectangle, Sekiranya salah satu sudut dalamannya bernilai 90º. Sisi yang membentuk 90º dipanggil catetos dan sebaliknya ke sudut kanan adalah hipotenus.

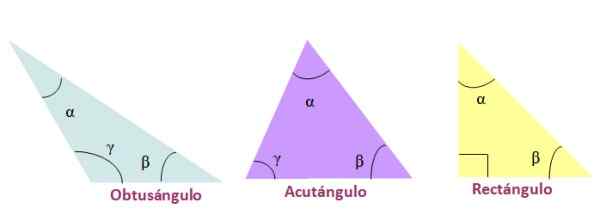Rajah 4. Klasifikasi segitiga dengan sudut dalaman mereka. Sumber: f. Zapata.

Congruence of Triangles

Apabila dua segitiga mempunyai bentuk yang sama dan saiz yang sama dikatakan bahawa mereka adalah kongruen. Sudah tentu kesesuaiannya berkaitan dengan kesamaan, jadi mengapa dalam geometri kita bercakap tentang "dua segitiga kongruen" dan bukannya "dua segitiga yang sama"?

Nah, lebih suka menggunakan istilah "kongruen" untuk berpegang pada kebenaran, kerana dua segitiga boleh mempunyai bentuk dan saiz yang sama, tetapi berorientasikan secara berbeza dalam satah (lihat Rajah 3). Dari sudut pandangan geometri, mereka tidak lagi sama dengan sama.

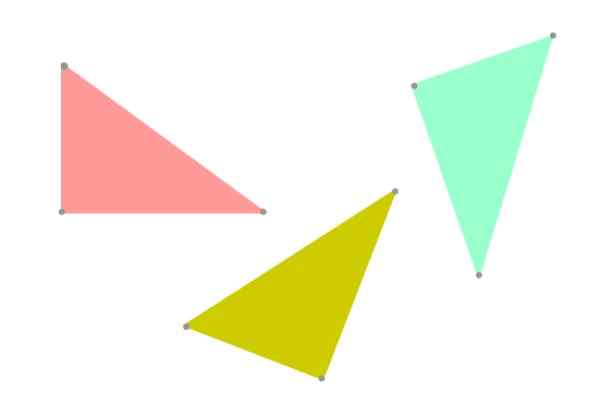Rajah 5. Segitiga kongruen, tetapi tidak semestinya sama, kerana orientasinya dalam satah berbeza. Sumber: f. Zapata.

Kriteria kongruen

Dua segitiga adalah kongruen jika mana -mana situasi berikut berlaku:

-Tiga sisi mengukur sama (sekali lagi ini adalah yang paling jelas).

-Mereka mempunyai dua sisi yang sama dan dengan sudut yang sama di antara mereka.

-Kedua -duanya mempunyai dua sudut dalaman yang sama dan sisi antara sudut ini adalah sama.

Seperti yang dapat dilihat, ia adalah mengenai dua segitiga yang memenuhi syarat -syarat yang diperlukan sehingga ketika membina mereka, bentuk dan saiznya sama persis.

Kriteria kongruen sangat berguna, kerana dalam praktik.

Persamaan segitiga

Segitiga sama dengan yang lain jika mereka mempunyai bentuk yang sama, walaupun mereka mempunyai saiz yang berbeza. Untuk memastikan bahawa bentuknya adalah sama, diperlukan sudut dalaman mempunyai nilai yang sama dan bahawa sisi adalah berkadar.

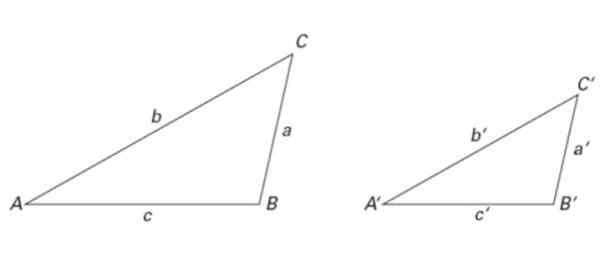Rajah 6. Dua segitiga yang serupa: saiz mereka berbeza tetapi perkadaran mereka adalah sama. Sumber: f. Zapata.

Segitiga Rajah 2 juga sama, dan juga dalam Rajah 6. Oleh itu:

∠ A = ∠ A ', ∠ B = ∠ B 'dan ∠ C = ∠ C '

Bagi pihak, sebab -sebab berikut persamaan dipenuhi:

a/a '= b/b' = c/c '

Sifat

Ciri -ciri asas segitiga adalah seperti berikut:

-Jumlah sudut dalaman mana -mana segitiga selalu 180º.

-Untuk mana -mana segitiga, jumlah sudut luarannya sama dengan 360 °.

Boleh melayani anda: penyelidikan asas: ciri, definisi, contoh

- Sudut luaran segitiga adalah sama dengan jumlah dua sudut dalaman yang tidak bersebelahan dengan sudut itu.

Teorem

Teorema pertama seperti itu

Mereka dikaitkan dengan ahli falsafah Yunani dan kisah matematik Miletus, yang membangunkan beberapa teorema yang berkaitan dengan geometri. Yang pertama dari mereka menetapkan perkara berikut:

Sekiranya beberapa garisan selari memotong dua garisan melintang, mereka menentukan segmen yang berkadar.

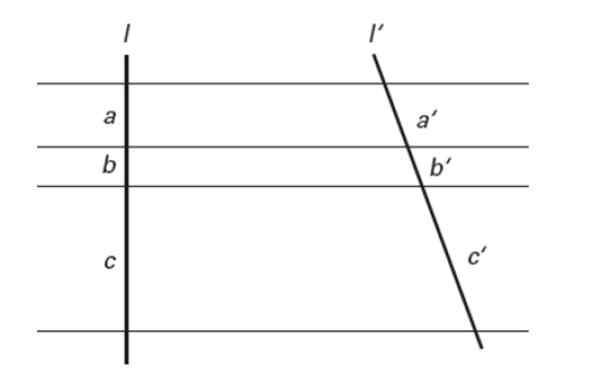Rajah 7. Teorem Tales. Sumber: f. Zapata.

Dalam kata lain:

a/a '= b/b' = c/c '

Teorem pertama seperti itu boleh digunakan untuk segitiga, contohnya terdapat segitiga biru ABC di sebelah kiri, yang dipotong oleh persamaan merah ke kanan:

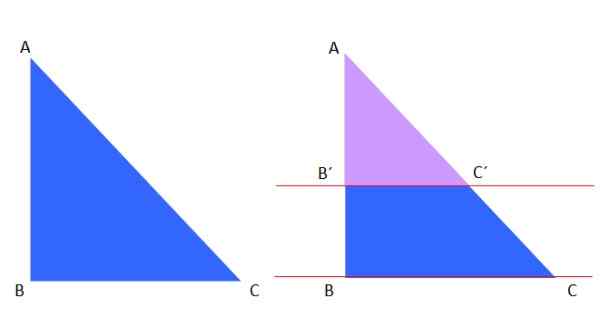Rajah 8. Teorem seperti itu dan segitiga yang serupa.

Segitiga ungu violet adalah serupa dengan segitiga biru ABC, oleh itu, mengikut teorem sedemikian, yang berikut boleh ditulis:

Ab '/ac' = ab/ac

Dan ia selaras dengan apa yang dijelaskan di atas dalam segmen persamaan segitiga. Dengan cara ini, garis selari juga boleh menegak atau selari dengan hipotenus dan segitiga yang serupa diperolehi.

Teorem kedua ini

Teorem ini juga merujuk kepada segitiga dan lilitan pusat atau, seperti yang ditunjukkan di bawah. Dalam angka ini, AC adalah diameter lilitan dan B adalah titik, yang berbeza dari A dan B.

Teorem kedua menyatakan bahawa:

Sudut antara segmen AB dan BC selalu 90º, oleh itu segitiga ABC adalah segi empat tepat.

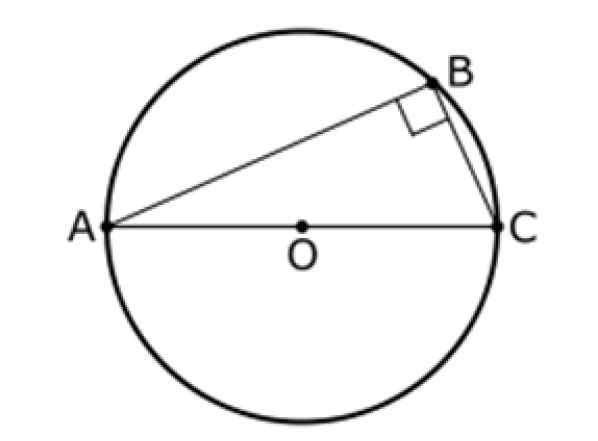Rajah 9. Teorem kedua seperti itu. Sumber: Wikimedia Commons. Inductiveload [domain awam].

Teorem Pythagoras

Ini adalah salah satu teorema paling terkenal dalam sejarah. Ini disebabkan oleh ahli matematik Yunani Pythagoras Samos (569 - 475 hingga. C.) dan boleh digunakan untuk segitiga yang betul. Mengatakan demikian:

Jumlah kuadrat panjang kategori segi tiga segi empat tepat, sama dengan panjang hipotenus tinggi ke dataran.

Jika kita mengambil sebagai contoh segitiga biru Rajah 8, atau segitiga violet, kerana kedua -duanya adalah segi empat tepat, maka dapat dikatakan:

Ac² = Ab² + BC² (Segitiga Biru)

AC '² = Ab '² + Bc '² (Segitiga Violet)

Kawasan segitiga

Kawasan segitiga diberikan oleh produk pangkalannya ke dan ketinggiannya h, dibahagikan dengan 2. Dan dengan trigonometri, ketinggian ini boleh ditulis sebagai H = b sinθ.

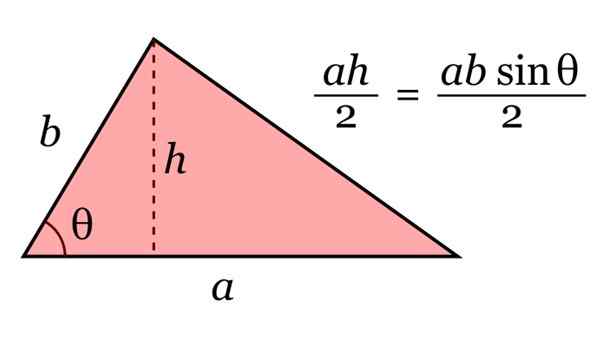Rajah 10. Kawasan segitiga. Sumber: Wikimedia Commons.

Contoh segitiga

Contoh 1

Dikatakan bahawa melalui teorem pertama, seperti itu berjaya mengukur ketinggian piramid besar di Mesir, salah satu dari 7 keajaiban dunia kuno, mengukur bayang -bayang yang diproyeksikan di atas tanah dan yang memproyeksikan kepentingan tanah.

Inilah skema prosedur yang diikuti oleh:

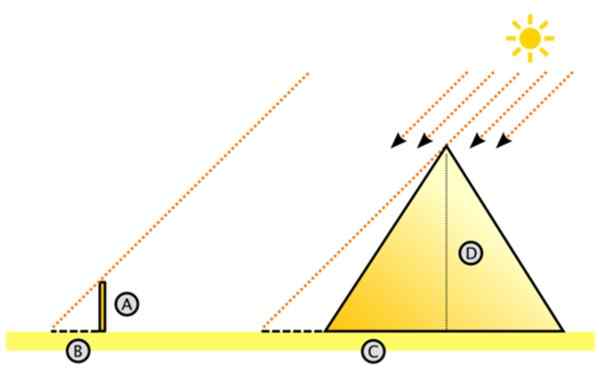Rajah 11. Skim untuk mengukur ketinggian piramid besar dengan persamaan segitiga. Sumber: Wikimedia Commons. Dake [CC BY-SA 3.0 (http: // creativeCommons.Org/lesen/by-sa/3.0/]]

Seperti itu kerana sinar matahari mempengaruhi selari. Dengan ini, dia membayangkan segitiga kanan kanan yang besar.

Terdapat ketinggian piramid dan c adalah jarak di tanah yang diukur dari pusat ke bayang -bayang yang diproyeksikan oleh piramid di lantai padang pasir. Mungkin sukar untuk mengukur C, tetapi ia pasti lebih mudah daripada mengukur ketinggian piramid.

Di sebelah kiri adalah segitiga kecil, dari kucing A dan B, di mana A adalah ketinggian pegangan yang tersekat secara menegak di lantai dan b adalah bayang -bayang projek. Kedua -dua panjang boleh diukur, sama seperti C (c adalah sama dengan panjang bayangan + separuh panjang piramid).

Boleh melayani anda: apakah rangsangan sentuhan?

Kemudian, dengan persamaan segitiga:

A/b = d/c

Dan ketinggian piramid besar ternyata: d = c.(A/b)

Contoh 2

Perisai pembinaan awam adalah struktur berdasarkan bar lurus kayu atau logam nipis, yang digunakan sebagai sokongan di banyak bangunan. Mereka juga dikenali sebagai kisi, kekalahan atau reticulated (Kekuda dalam Bahasa Inggeris).

Di dalamnya segitiga selalu hadir, kerana bar dihubungkan dengan titik yang disebut nod, yang mungkin ditetapkan atau diartikulasikan.

Rajah 12. Segitiga terdapat di bingkai jambatan ini. Sumber: Pxhere.

Contoh 3

Kaedah yang dikenali sebagai triangulasi membolehkan anda mendapatkan lokasi titik -titik yang tidak dapat diakses dengan mengetahui jarak yang lebih mudah untuk diukur, dengan syarat segitiga terbentuk yang termasuk di antara simpulnya lokasi yang dikehendaki.

Sebagai contoh, dalam angka berikut yang anda ingin tahu di mana titik laut adalah kapal, dilambangkan sebagai b.

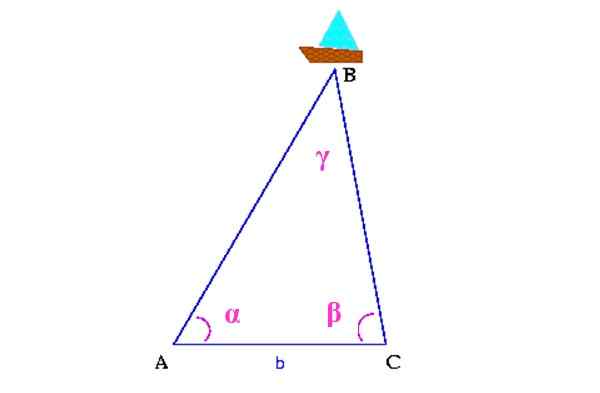Rajah 13. Skim Triangulasi untuk mencari kapal. Sumber: Wikimedia Commons. Colette [CC BY-SA 3.0 (http: // creativeCommons.Org/lesen/by-sa/3.0/]]

Pertama, jarak antara dua mata di pantai diukur, yang dalam angka adalah A dan C. Kemudian anda perlu menentukan sudut α dan β, dengan bantuan a Theodolite, Peranti yang berfungsi untuk mengukur sudut menegak dan mendatar.

Dengan semua maklumat ini segitiga dibina di atas puncak atasnya adalah kapal. Ia akan mengurangkan sudut γ, dengan cara.

Latihan

Latihan 1

Dalam angka yang ditunjukkan, sinar matahari selari. Dengan cara ini, pokok 5 -meter tinggi memproyeksikan bayangan 6 -meter di tanah. Pada masa yang sama, bayang -bayang bangunan adalah 40 meter. Berikutan teorem sedemikian, cari ketinggian bangunan.

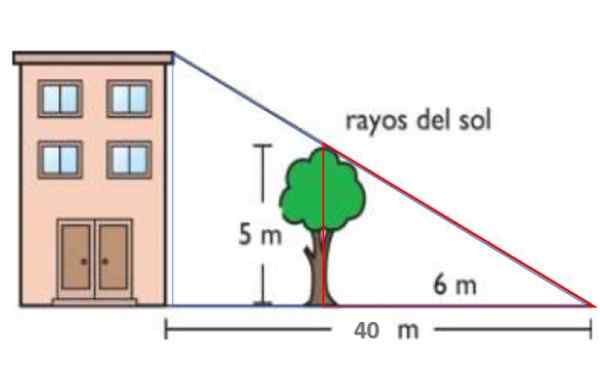Rajah 14. Skim untuk tahun diselesaikan 1. Sumber: f. Zapata.

Penyelesaian

Segitiga merah masing -masing mempunyai sisi 5 dan 6 meter, manakala biru mempunyai ketinggian h -ketinggian bangunan dan asas 40 meter. Kedua -dua segitiga adalah serupa, oleh itu:

H / 40 = 5/6 → H = 40.(5/6) m = 33.3 m

Latihan 2

Anda perlu mengetahui jarak mendatar antara dua mata Ke dan B, Tetapi mereka terletak di kawasan yang sangat tidak teratur.

Kira -kira di titik tengah (p_m) Dari tanah ini menjadi terkenal 1 menonjol.75 meter tinggi. Sekiranya ukuran pita menunjukkan panjang 26 meter yang diukur dari A ke keunggulan, dan 27 meter dari B ke titik yang sama, cari jarak Ab.

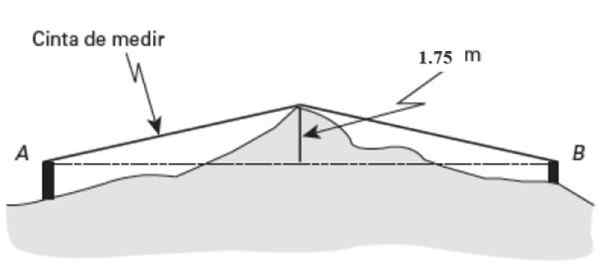Rajah 15. Skim untuk latihan diselesaikan 2. Sumber: Jiménez, R. Matematik II. Geometri dan trigonometri.

Penyelesaian

Teorem Pythagoras digunakan untuk salah satu daripada dua segi empat segi segi empat tepat dalam angka tersebut. Bermula dengan yang ada di sebelah kiri:

Hypotenuse = C = 26 meter

Ketinggian = a = 1.75 meter

Ap_m = (26² - 1.75²)^1/2 = 25.94 m

Sekarang Pythagoras digunakan di segitiga yang betul, kali ini c = 27 meter, a = 1.75 meter. Dengan nilai -nilai ini:

BP_m= (27² - 1.75²)^1/2 = 26.94 m

Jarak AB menambah hasil ini:

AB = 25.94 M +26.94 m = 52.88 m.

Rujukan

1. Baldor, j. Ke. 1973.Geometri rata dan ruang. Kebudayaan Amerika Tengah.
2. Barredo, d. Geometri segitiga. Pulih dari: ficus.pntic.Mec.adalah.
3. Jiménez, r. 2010. Matematik II. Geometri dan trigonometri. Edisi kedua. Pearson.
4. Wentworth, g. Geometri Planet. Pulih dari: gutenberg.org.
5. Wikipedia. Segitiga. Pulih dari: Adakah. Wikipedia.org.